
Starting from simple vector addition, learn how to write Triton kernels and explore performance tuning techniques.
Vector Add in Triton
Single-threaded Version
Element-wise addition:
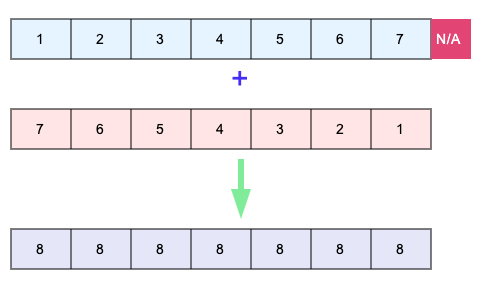
Triton Implementation
In Triton, a vector addition kernel achieves efficiency by partitioning vectors into multiple blocks and computing them in parallel across threads within each Grid. Each thread is responsible for loading corresponding elements from two vectors, adding them, and storing the result.
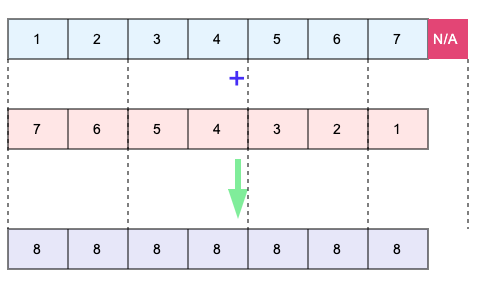
Core Steps
- Parallel Computation: Threads in each Grid independently process a segment of the vector.
- Load Elements: Each thread loads corresponding elements from Vector A and Vector B.
- Element Addition: Perform the addition on loaded elements.
- Store Result: Store the result in the output vector.
Using tl.constexpr
tl.constexpr is used to declare compile-time constants. This means the variable’s value is determined at compile time rather than runtime, allowing the compiler to perform more aggressive optimizations to boost kernel efficiency.
@triton.jit
def kernel_vector_addition(a_ptr, b_ptr, out_ptr,
num_elems: tl.constexpr,
block_size: tl.constexpr):
# Kernel codeIn the code above, num_elems and block_size are declared as compile-time constants, enabling Triton to optimize the kernel during the compilation phase.
Determining Current Block and Program ID
Each thread block in Triton has a unique Program ID identifying its position. Using tl.program_id, we can determine the block’s ID and calculate the data offset for processing.
pid = tl.program_id(axis=0)
block_start = pid * block_sizeHandling the Last Block
Since the vector length might not be divisible by the block size, the final block might only require some threads to work. Masking ensures only valid threads perform computations, preventing invalid memory access.
Role of Masking
Triton provides masking to disable threads that are not needed (NA threads in the final Grid).
mask = thread_offsets < num_elems
a_pointers = tl.load(a_ptr + thread_offsets, mask=mask, other=0.0)
b_pointers = tl.load(b_ptr + thread_offsets, mask=mask, other=0.0)The ceil_div Function
ceil_div calculates the number of blocks needed to cover all elements, even if the length isn’t perfectly divisible. For example, if vec_size=10 and block_size=3, ceil_div(10, 3)=4 ensures all 10 elements are processed.
def ceil_div(x: int, y: int) -> int:
return (x + y - 1) // yEssentially, this function efficiently implements “rounding up.”
Numerical Validation
After implementing the kernel, verifying numerical accuracy is crucial. Comparing results with PyTorch’s native addition confirms the Triton implementation’s correctness.
def verify_numerics() -> bool:
torch.manual_seed(2020) # seed both CPU and GPU
vec_size = 8192
a = torch.rand(vec_size, device='cuda')
b = torch.rand_like(a)
torch_res = a + b
triton_res = vector_addition(a, b)
fidelity_correct = torch.allclose(torch_res, triton_res)
print(f"{fidelity_correct=}")
return fidelity_correct
Validation confirms our Triton implementation matches PyTorch’s native numerical precision.
Full Kernel implementation:
@triton.jit
def kernel_vector_addition(a_ptr, b_ptr, out_ptr,
num_elems: tl.constexpr,
block_size: tl.constexpr,):
pid = tl.program_id(axis=0)
block_start = pid * block_size
thread_offsets = block_start + tl.arange(0, block_size)
mask = thread_offsets < num_elems
a_pointers = tl.load(a_ptr + thread_offsets, mask=mask)
b_pointers = tl.load(b_ptr + thread_offsets, mask=mask)
res = a_pointers + b_pointers
tl.store(out_ptr + thread_offsets, res, mask=mask)
def ceil_div(x: int,y: int) -> int:
return (x + y - 1) // y
def vector_addition(a: torch.Tensor, b: torch.Tensor) -> torch.Tensor:
output_buffer = torch.empty_like(a)
assert a.is_cuda and b.is_cuda
num_elems = a.numel()
assert num_elems == b.numel()
block_size = 1024
grid_size = ceil_div(num_elems, block_size)
grid = (grid_size,)
num_warps = 8
kernel_vector_addition[grid](a, b, output_buffer,
num_elems,
block_size,
num_warps=num_warps
)
return output_bufferBenchmarking and Tuning
To evaluate performance, we’ll run benchmarks and explore tuning methods.
Benchmark API
Triton offers a rich benchmarking API to measure execution time and throughput. Example using triton.testing.perf_report:
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['size'],
x_vals=[2**i for i in range(10, 28)],
x_log=True,
line_arg='provider',
line_vals=['triton', 'torch'],
line_names=["Triton", "Torch"],
styles=[('blue', '-'), ('green', '-')],
ylabel='GB/s',
plot_name='vector-add-performance',
args={},
)
)
def benchmark(size, provider):
x = torch.rand(size, device='cuda', dtype=torch.float32)
y = torch.rand(size, device='cuda', dtype=torch.float32)
quantiles = [0.5, 0.2, 0.8]
if provider == 'torch':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: x + y, quantiles=quantiles)
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: vector_addition(x, y), quantiles=quantiles)
def gbps(ms):
return 12 * size / ms * 1e-06
return gbps(ms), gbps(max_ms), gbps(min_ms)Performance report:
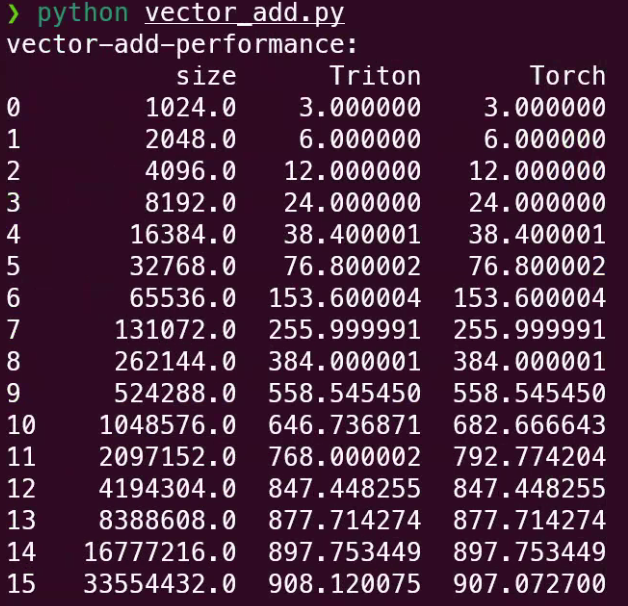
Comparison:
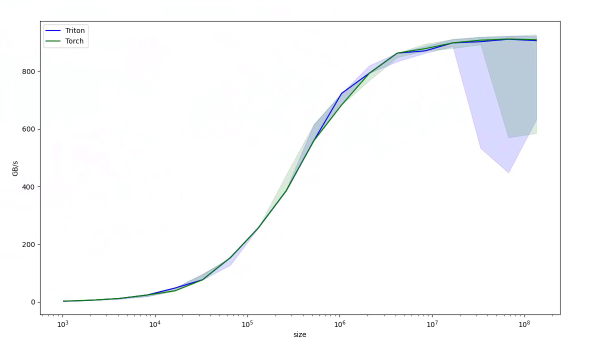
Vector addition is a simple kernel, making it harder to gain significant advantages over PyTorch’s already highly optimized CUDA/cuBLAS implementations for such standard operations.
Tuning Parameters: Num Warps & Block Size
The key to tuning is properly configuring the number of warps and the block size. Warps are basic execution units in GPUs; ideal configurations maximize parallel utilization and efficiency.
block_size = 1024 # Elements per block. Larger blocks reduce block count but increase load per block.
grid_size = ceil_div(num_elems, block_size)
grid = (grid_size,)
num_warps = 8 # Warps per block. Proper configuration optimizes scheduling and resource usage.The previous section (Softmax in OpenAI Triton) showed how to dynamically adjust these parameters via the driver:
# Compute block_size as smallest power of 2 >= cols
block_size = triton.next_power_of_2(cols)
# Adjust num_warps based on block_size
num_warps = 4 # 32 threads per warp
if block_size > 2047:
num_warps = 8
if block_size > 4095:
num_warps = 16References
Special thanks to:
- SOTA Deep Learning Tutorials - YouTube
- Triton’s documentation
- o1-preview language model, master of SVG drawings.