Let's build AlphaZero

This article is a digestion and understanding of articles, video tutorials, and code implementations such as Sunrise: Understanding AlphaZero, MCTS, Self-Play, UCB from Scratch.

This article will start from the design principles of AlphaGo, gradually revealing how to build an AI Gomoku system that can surpass human capabilities by deeply understanding the two core mechanisms: MCTS and Self-Play.

AlphaGo: From Imitation to Surpassing#

Evolution Path of AlphaGo#

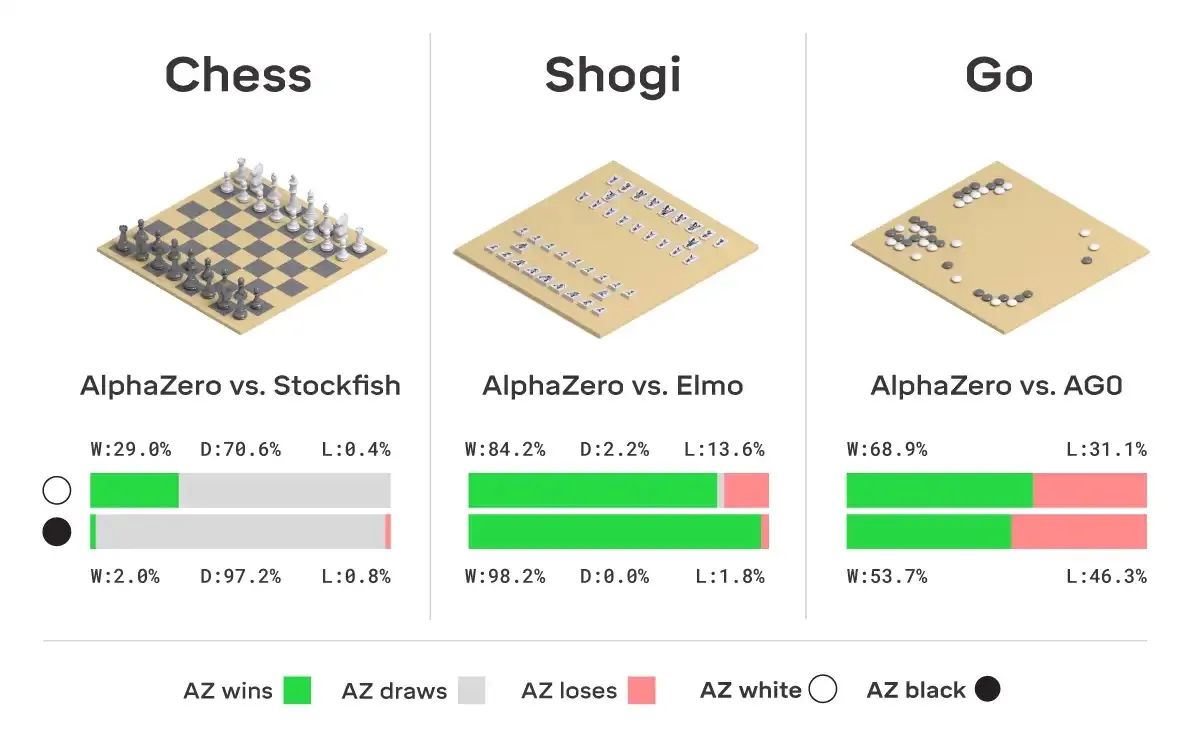
The possible board configurations in Go exceed the number of atoms in the universe, rendering traditional exhaustive search methods completely ineffective. AlphaGo addresses this problem through a phased approach: first learning human knowledge, then continuously evolving through self-play.

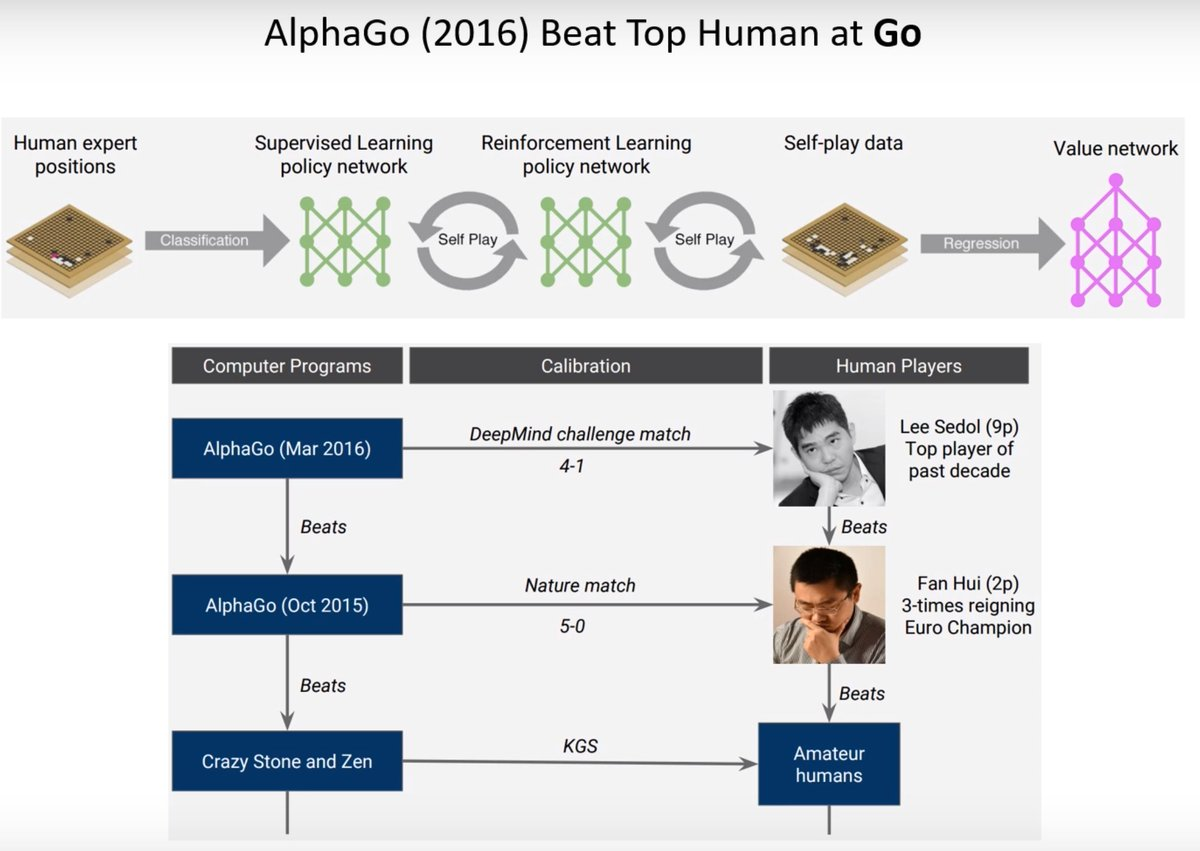
This evolutionary process can be divided into three layers:

Imitating human masters
Self-play enhancement
Learning to evaluate the situation

Core Components#

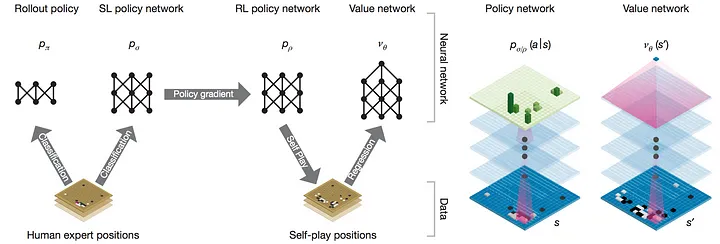
Rollout Policy#

The leftmost lightweight policy network, used for quick evaluation, has lower accuracy but high computational efficiency.

SL Policy Network#

The supervised learning policy network $P_{\sigma}$ learns to play by imitating human game records:

Input: Board state
Output: Probability distribution of the next move imitating human experts
Training data: 160,000 games, approximately 30 million moves

RL Policy Network#

Similar to when your skill reaches a certain level, you start reviewing your games and playing against yourself, discovering new tactics and deeper strategies. The RL network $P_{\rho}$ is initialized from the SL network, which has already surpassed human capabilities and can find many powerful strategies that humans have not discovered.

This stage generates a large amount of self-play data, with the input still being the board state, and the output is the move strategy improved through reinforcement learning.
Self-play with the historical version of the policy network $p_\pi$ , where the network adjusts parameters through the "win" signal, reinforcing the moves that lead to victory:

\sum_{t} z(\tau) \log p(a_t \mid s_t; \rho)

where:

$\tau$ is the game sequence $(s_0,a_0,s_1,a_1,...)$
$z(\tau)$ is the win-loss label (win is positive, loss is negative)

Value Network#

The value network $v_\theta$ learns to evaluate the situation and can be a CNN:

Training objective: Minimize the mean squared error

\sum_{i} (z - v_\theta(s))^2

$z$ : Final win-loss result
$v_\theta(s)$ : Predicted winning probability

Supplementary Explanation#

About the relationship between $P_\rho$ and $v_\theta$ :

The policy network $P_\rho$ provides specific move probabilities to guide the search.
The value network $v_\theta$ provides situation evaluations, reducing unnecessary simulations in the search tree.
The combination of both allows MCTS to not only explore high win-rate paths faster but also significantly improve overall playing strength.

AlphaGo's MCTS Implementation#

Selection Phase#

Combining exploration and exploitation:

a_t = \arg\max_a Q(s_t, a) + u(s_t, a)

u(s_t, a) \propto \frac{P(s_t, a)}{1 + N(s_t, a)}

where:

$Q(s_t, a)$ : Long-term return estimate
$u(s_t, a)$ : Exploration reward
$P(s_t, a)$ : Prior probability output from the policy network
$N(s_t, a)$ : Visit count

Simulation and Evaluation#

In the original MCTS algorithm, the role of the simulation phase is to play random games from the leaf nodes (newly expanded nodes) using a fast rollout policy until the game ends, then obtaining a reward based on the outcome of the game. This reward is passed back to the nodes in the search tree to update their value estimates (i.e., $Q(s, a)$ ).

This implementation is simple and direct, but the rollout policy is usually random or based on simple rules, which may result in poor simulation quality. It can only provide short-term information and does not effectively combine global strategic evaluations.

AlphaGo, however, combines the Value Network $v_\theta$ with the rollout policy during the simulation phase. The Value Network provides more efficient leaf node estimates and global capability assessments, while the rollout policy captures local short-term effects through rapid simulations.

Using the hyperparameter $\lambda$ to balance $v_\theta(s_L)$ and $z_L$ , it considers both local simulations and global evaluations. The evaluation function:

V(s_L) = (1 - \lambda)v_\theta(s_L) + \lambda z_L

Backpropagation#

During n times of MCTS, the node visit count updates (where $\mathbb{I}$ is the indicator function, visiting is 1):

N(s_t, a) = \sum_{i=1}^{n} \mathbb{I}(s, a, i)

Q value updates, i.e., executing a to node $s_t$ 's long-term expected return:

Q(s_t, a) = \frac{1}{N(s_t, a)} \sum_{i=1}^{n} \mathbb{I}(s, a, i) V(s_L^i)

Summary#

Structural Innovation:
- The policy network provides prior knowledge
- The value network provides global evaluation
- MCTS provides tactical verification
Training Innovation:
- Starting from supervised learning
- Surpassing the teacher through reinforcement learning
- Self-play generates new knowledge
MCTS Improvements:
- Using neural networks to guide the search
- The Policy Network provides prior probabilities for exploration direction, and the Value Network enhances the accuracy of leaf node evaluations.
- This combination of value network and rollout evaluation not only reduces the search width and depth but also significantly improves overall performance.
- Efficient exploration-exploitation balance

This design enables AlphaGo to find efficient solutions in a vast search space, ultimately surpassing human levels.

Heuristic Search and MCTS#

MCTS is like an ever-evolving explorer, seeking the best path in a decision tree.

Core Idea#

What is the essence of MCTS? Simply put, it is a "learn while playing" process. Imagine you are playing a brand new board game:

At first, you will try various possible moves (exploration)
Gradually, you discover that certain moves work better (exploitation)
Balancing between exploring new strategies and exploiting known good strategies

This is precisely what MCTS does, but it systematizes this process mathematically. It is a rollout algorithm that guides strategy selection by accumulating value estimates from Monte Carlo simulations.

Algorithm Process#

Monte Carlo Tree Search - YouTube This teacher explains the MCTS process very well.

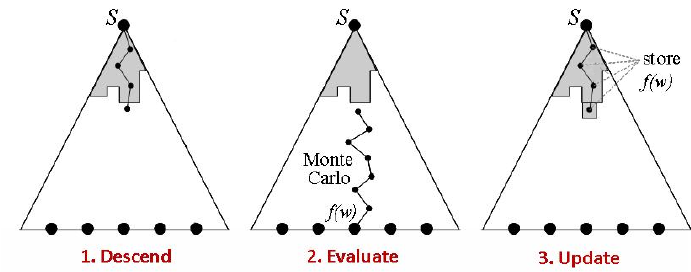
The elegance of MCTS lies in its four simple yet powerful steps, which I will introduce using two perspectives, A and B:

Selection
- A: Do you know how children learn? They always hover between the known and the unknown. MCTS is similar: starting from the root node, it uses the UCB (Upper Confidence Bound) formula to weigh whether to choose a known good path or explore new possibilities.
- B: Starting from the root node, select a subsequent node from the current node based on a specific strategy. This strategy is usually based on the search history of the tree, selecting the most promising path. For example, at each node, we execute action $a$ based on the current strategy $\pi(s)$ to balance exploration and exploitation, gradually delving deeper.
Expansion
- A: Like an explorer opening up new areas on a map, when we reach a leaf node, we will expand downwards, creating new possibilities.
- B: When the selected node still has unexplored child nodes, we expand new nodes under this node based on the set of possible actions. The purpose of this process is to increase the breadth of the decision tree, gradually generating possible decision paths. Through this expansion operation, we ensure that the search covers more possible state-action pairs $(s,a)$ .
Simulation
- A: This is the most interesting part. Starting from the new node, we conduct a "hypothetical" game until it ends. It's like playing chess while mentally simulating "if I move this way, my opponent will move that way...".
- B: Starting from the currently expanded node, perform random simulations (rollouts), sampling along the current strategy $\pi(s)$ in the MDP environment until reaching a terminal state. This process provides a reward estimate from the current node to the endpoint, offering numerical evidence for the quality of the path.
Backpropagation
- A: Finally, we return the results along the path, updating the statistics of each node. It's like saying, "Hey, I tried this path, and it worked pretty well (or not so well)."
- B: After completing the simulation, backpropagate the estimated reward of this simulation to all the nodes traversed to update their values. This process accumulates historical reward information, making future choices more accurately trend towards high-reward paths.

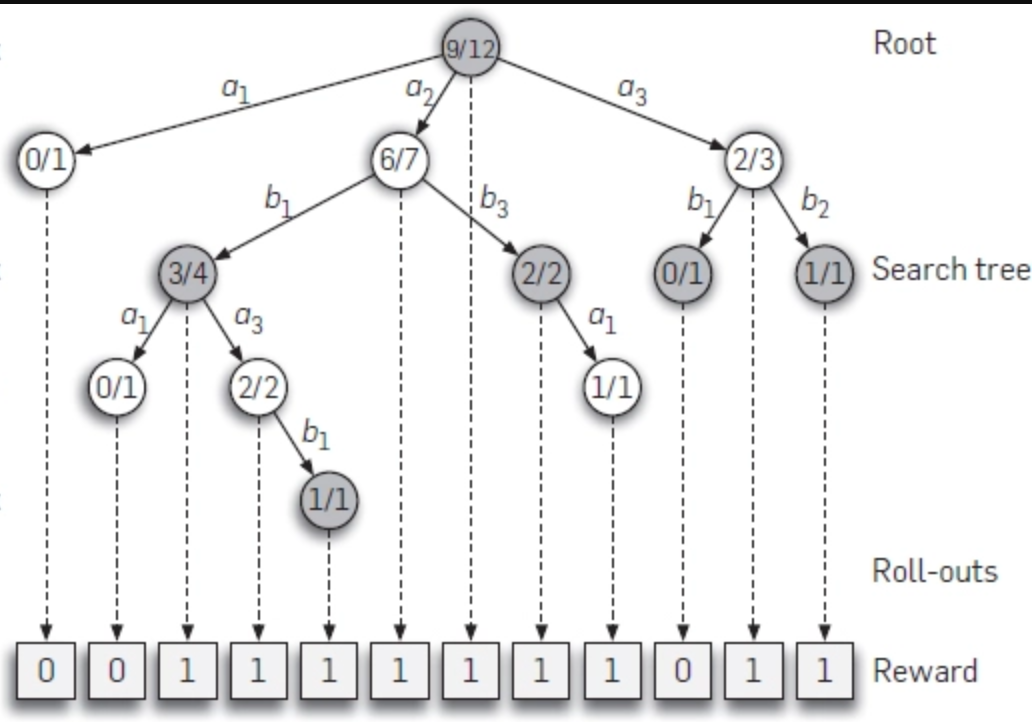
UCB1: The Perfect Balance of Exploration and Exploitation#

Here, the UCB1 formula, which is the soul of MCTS, deserves special mention:

UCB1 = X̄ᵢ + C × \sqrt{(ln(N)/nᵢ)}

Let's break it down:

$X̄ᵢ$ is the average return (exploitation term)
$\sqrt{(ln(N)/nᵢ)}$ is the uncertainty measure (exploration term)
$C$ is the exploration parameter

Like a good investment portfolio, it should focus on known good opportunities while remaining open to new ones (exploration-exploitation trade-off).

Best Multi-Armed Bandit Strategy? (feat: UCB Method) This video explains Multi-Armed Bandit and UCB Method very well, and I borrow the example used by this teacher:

A Foodie Trying to Understand UCB#

Imagine you just arrived in a city with 100 restaurants to choose from, and you have 300 days. Each day, you need to choose a restaurant to dine in, hoping to average the best food over these 300 days.

ε-greedy Strategy: Simple but Not Smart#

This is like deciding by rolling a die:

90% of the time (ε=0.1): Go to the known best restaurant (exploitation)
10% of the time: Randomly try a new restaurant (exploration)

def epsilon_greedy(restaurants, ratings, epsilon=0.1):
    if random.random() < epsilon:
        return random.choice(restaurants)  # Exploration
    else:
        return restaurants[np.argmax(ratings)]  # Exploitation

The effect is:

Exploration is completely random, possibly revisiting known bad restaurants
The exploration ratio is fixed and does not adjust over time
It does not consider the impact of visit counts

UCB Strategy: A Smarter Choice Trade-off#

The UCB formula in restaurant selection means:

Score = Average Score + C × \sqrt{ln(Total Visit Days)/Visits of This Restaurant}

For example, consider the situation of two restaurants on day 100:

Restaurant A:

Visited 50 times, average score 4.5
UCB score = $4.5 + 2×\sqrt{ln(100)/50} ≈ 4.5 + 0.6 = 5.1$

Restaurant B:

Visited 5 times, average score 4.0
UCB score = $4.0 + 2×\sqrt{ln(100)/5} ≈ 4.0 + 1.9 = 5.9$

Although Restaurant B has a lower average score, it receives a higher exploration reward due to fewer visits and higher uncertainty.

Code implementation:

class Restaurant:
    def __init__(self, name):
        self.name = name
        self.total_rating = 0
        self.visits = 0
        
def ucb_choice(restaurants, total_days, c=2):
    # Ensure each restaurant is visited at least once
    for r in restaurants:
        if r.visits == 0:
            return r
            
    # Use UCB formula to choose a restaurant
    scores = []
    for r in restaurants:
        avg_rating = r.total_rating / r.visits
        exploration_term = c * math.sqrt(math.log(total_days) / r.visits)
        ucb_score = avg_rating + exploration_term
        scores.append(ucb_score)
        
    return restaurants[np.argmax(scores)]

Why UCB is Better?#

Adaptive Exploration
- Restaurants with fewer visits receive higher exploration rewards
- As the total days increase, the exploration term gradually decreases for better exploitation
Balanced Time Investment
- It won't waste too much time on clearly inferior restaurants
- It will reasonably distribute visit counts among similarly potential restaurants
Theoretical Guarantee
- Regret Bound (the gap from the optimal choice) grows logarithmically over time
- 300 days of exploration is sufficient to find the best few restaurants

Back to MCTS:

Why is MCTS So Powerful?#

Efficiently Handles Combinatorial Explosion: MCTS does not need to exhaustively search all possibilities like Minimax, but focuses on the most promising branches, enabling it to effectively handle problems with huge branching factors.
Adaptive Search: MCTS dynamically adjusts its search strategy, allocating more resources to more promising areas, thus finding good solutions faster.
Balances Exploration and Exploitation: Through the UCB formula, MCTS achieves a balance between exploring new possibilities and exploiting known good choices, avoiding getting stuck in local optima.
No Domain Knowledge Required: MCTS does not rely on specific domain expertise, learning solely from game rules and simulation results, making it widely applicable.
Can Stop Anytime: MCTS is a "anytime" algorithm, which can be interrupted at any time and return the current best solution, which is crucial for real-time applications.

AlphaZero: From MCTS to Self-Evolution#

AlphaZero is a general reinforcement learning algorithm launched by DeepMind after AlphaGo, capable of learning from scratch and ultimately surpassing professional levels through self-play without using human game records.

AlphaZero improves upon traditional MCTS by introducing neural networks to guide the search:

Policy Prior: Uses neural networks to predict the prior probabilities of each action, making search more efficient.
Value Evaluation: At leaf nodes, it uses the value predictions from neural networks instead of random simulations, reducing computational costs.

Below, we will implement an AI that can learn in this way using Gomoku as an example. Here, we learn from and reference the excellent implementation of schinger/alphazero.py.

Designing the Game Environment#

Before implementing AlphaZero, we need to define the game environment.

Defining the Game Interface#

In AlphaZero, the neural network receives the current board state and outputs a policy vector $\boldsymbol{P}$ representing the probabilities of each action, as well as a scalar value $v$ representing the current player's winning probability prediction.

To enable MCTS and neural networks to interact with the game universally, we need to define a consistent game interface.

class GomokuGame:
    def __init__(self, n=15):
        self.n = n  # Board size, default 15x15

    def getInitBoard(self):
        """
        Returns the initial board state, all positions are empty.
        """
        b = Board(self.n)
        return np.array(b.pieces)

    def getBoardSize(self):
        """
        Returns the size of the board, i.e., (n, n).
        """
        return (self.n, self.n)

    def getActionSize(self):
        """
        Returns the total number of actions, which is n * n, as each cell can be an action.
        """
        return self.n * self.n

    def getNextState(self, board, player, action):
        """
        Executes an action and returns the next board state and the next player.

        Parameters:
        - board: Current board state
        - player: Current player (1 or -1)
        - action: Current action, 0 ~ n*n-1

        Returns:
        - (next_board, next_player): The board and next player after executing the action
        """
        b = Board(self.n)
        b.pieces = np.copy(board)
        # Convert action to coordinates (x, y)
        move = (action // self.n, action % self.n)
        b.execute_move(move, player)
        return (b.pieces, -player)

Unified interface: Allows our MCTS and neural networks to be reused across different games, requiring only the implementation of the specific game logic.
Board representation: Uses a two-dimensional array to represent the board, facilitating processing and visualization.

Core Algorithm Implementation#

Dual-Head Neural Network#

Network Structure#

In AlphaZero, we use a unified dual-head neural network to simultaneously predict policy (policy) and value (value). This neural network receives the current board state to compute outputs:

• $p$ : The probability distribution output by the policy head, representing the selection probability of each possible action in state $s$ . This policy head combines with MCTS search to generate stronger decisions.
• $v$ : The value head outputs a scalar, representing the predicted value of the current board state $s$ (the probability of winning).

import torch
import torch.nn as nn
import torch.nn.functional as F

class AlphaZeroNNet(nn.Module):
    def __init__(self, game, args):
        """
        Parameters:
        - game: Game object providing information such as board size and action space size.
        - args: Contains parameters for network structure, such as number of channels, dropout probability, etc.
        """
        super(AlphaZeroNNet, self).__init__()
        self.board_x, self.board_y = game.getBoardSize()  # Board size
        self.action_size = game.getActionSize()           # Action space size
        self.args = args

        # Convolutional layer blocks
        self.conv_layers = nn.Sequential(
            nn.Conv2d(1, args.num_channels, kernel_size=3, padding=1),
            nn.BatchNorm2d(args.num_channels),
            nn.ReLU(),
            nn.Conv2d(args.num_channels, args.num_channels, kernel_size=3, padding=1),
            nn.BatchNorm2d(args.num_channels),
            nn.ReLU(),
            nn.Conv2d(args.num_channels, args.num_channels, kernel_size=3),
            nn.BatchNorm2d(args.num_channels),
            nn.ReLU(),
            nn.Conv2d(args.num_channels, args.num_channels, kernel_size=3),
            nn.BatchNorm2d(args.num_channels),
            nn.ReLU(),
        )

        # Calculate the output size of the convolutional layers
        conv_output_size = self._get_conv_output_size()

        # Fully connected layer blocks
        self.fc_layers = nn.Sequential(
            nn.Linear(conv_output_size, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(args.dropout),
            nn.Linear(1024, 512),
            nn.BatchNorm1d(512),
            nn.ReLU(),
            nn.Dropout(args.dropout),
        )

        # Policy head: Outputs the log probabilities of each action
        self.policy_head = nn.Linear(512, self.action_size)

        # Value head: Outputs the value estimate of the current state
        self.value_head = nn.Linear(512, 1)

    def _get_conv_output_size(self):
        """
        Calculates the number of features output by the convolutional layers.
        """
        dummy_input = torch.zeros(1, 1, self.board_x, self.board_y)
        output_feat = self.conv_layers(dummy_input)
        n_size = output_feat.view(1, -1).size(1)
        return n_size

    def forward(self, s):
        """
        Forward propagation function.

        Parameters:
        - s: Input board state, shape (batch_size, board_x, board_y).

        Returns:
        - log_policies: Log probabilities of the policy, shape (batch_size, action_size).
        - values: Value estimates, shape (batch_size, 1).
        """
        # Adjust input shape
        s = s.view(-1, 1, self.board_x, self.board_y)  # (batch_size, 1, board_x, board_y)

        # Convolutional layers extract features
        s = self.conv_layers(s)  # (batch_size, num_channels, new_board_x, new_board_y)

        # Flatten the output of the convolutional layers
        s = s.view(s.size(0), -1)  # (batch_size, conv_output_size)

        # Fully connected layers extract high-level features
        s = self.fc_layers(s)  # (batch_size, 512)

        # Policy head output
        policies = self.policy_head(s)  # (batch_size, action_size)
        log_policies = F.log_softmax(policies, dim=1)

        # Value head output
        values = self.value_head(s)  # (batch_size, 1)
        values = torch.tanh(values)  # Limit the value to [-1, 1]

        return log_policies, values

Convolutional layers extract features: Through multiple convolutional layers, spatial features of the board are extracted.
Fully connected layers output: The features are flattened and passed through fully connected layers to output policy and value separately.
Activation functions:
- The policy output uses log_softmax, facilitating subsequent cross-entropy loss calculations.
- The value output uses tanh, limiting the value to $[-1, 1]$ .

Loss Function#

The training objective is defined through the following loss function to simultaneously train the network's policy and value evaluation capabilities:

l = (z - v)^2 - \pi \log p + c \| \theta \|^2

• $(z - v)^2$ : Value loss, requiring the network output $v$ to be as close as possible to the game result $z$ (win is +1, loss is -1, draw is 0).
• $- \pi \log p$ : Policy loss, through cross-entropy, requiring the network output policy $p$ to match the final policy $\pi$ obtained from MCTS as closely as possible.
• $c \| \theta \|^2$ : L2 regularization term to prevent overfitting, keeping the weight scale of model parameters $\theta$ appropriate.

MCTS Class#

class MCTS:
    def __init__(self, game, nnet, args):
        self.game = game         # Game environment
        self.nnet = nnet         # Neural network
        self.args = args         # Parameters
        self.Qsa = {}            # Store Q values: Q(s,a)
        self.Nsa = {}            # Store edge visit counts: N(s,a)
        self.Ns = {}             # Store node visit counts: N(s)
        self.Ps = {}             # Store policy priors: P(s,a)

        self.Es = {}             # Store game end information: E(s)
        self.Vs = {}             # Store valid actions: V(s)

One highlight here is the use of a caching mechanism: using dictionaries to cache computed results, avoiding redundant calculations and improving efficiency.

Valid Action Mask#

In many games, certain actions are illegal in specific states. For example, in Gomoku, if a position is already occupied, placing a piece there is illegal. Therefore, ensuring that only valid actions are considered is crucial for the correctness and efficiency of the algorithm. This is achieved through the valid action mask.

In the search method, when we reach a leaf node and need to use the neural network for predictions, we process the policy output from the neural network using the valid mask to mask illegal actions.

if s not in self.Ps: # Not in the policy prior storage P(s,a)
    # Leaf node, expand based on the policy output from the neural network
    self.Ps[s], v = self.nnet.predict(canonicalBoard)
    valids = self.game.getValidMoves(canonicalBoard, 1)  # Get the mask for valid actions, 1 for valid
    self.Ps[s] = self.Ps[s] * valids  # Mask illegal actions
    sum_Ps_s = np.sum(self.Ps[s])
    
    if sum_Ps_s > 0:
        self.Ps[s] /= sum_Ps_s  # Normalize policy probabilities
    else:
        # All actions are masked, perform uniform distribution
        self.Ps[s] = self.Ps[s] + valids
        self.Ps[s] /= np.sum(self.Ps[s])

    self.Vs[s] = valids  # Store the mask for valid actions
    self.Ns[s] = 0       # Initialize state visit count
    return v

PUCT#

A variant of the UCB formula specifically for MCTS.

In AlphaZero, MCTS uses the outputs from the neural network to guide the search direction. During the search process, the neural network selects actions using the improved upper confidence limit formula PUCT (Polynomial Upper Confidence Trees for Trees), introducing prior probabilities $P(s, a)$ , which allows MCTS to leverage external knowledge (policy network) to guide the search:

U(s, a) = Q(s, a) + c_{puct} \cdot P(s, a) \cdot \frac{\sqrt{N(s)}}{1 + N(s, a)}

where:

$Q(s, a)$ is the average value of choosing action $a$ in state $s$ .
$P(s, a)$ is the prior probability provided by the neural network.
$N(s)$ and $N(s, a)$ are the visit counts for state $s$ and edge $(s, a)$ , respectively.
$c_{puct}$ is a constant that controls the degree of exploration. The combination of the exploration term encourages the selection of actions with high prior probabilities but low visit counts.

cur_best = -float('inf') # Record the current maximum U value
best_act = -1            # Record the action with the maximum U value

# Iterate through all possible actions
for a in range(self.game.getActionSize()):
    if valids[a]: 
        # For valid actions, calculate the PUCT value
        if (s, a) in self.Qsa:
            # If (s, a) has been visited before, use the computed Q value and visit count
            u = self.Qsa[(s, a)] + self.args.cpuct * self.Ps[s][a] * \
                math.sqrt(self.Ns[s]) / (1 + self.Nsa[(s, a)])
        else:
            # If it is an unvisited node, the Q value is 0, encouraging exploration
            u = self.args.cpuct * self.Ps[s][a] * math.sqrt(self.Ns[s] + 1e-8) # Give higher U value to unvisited actions, avoiding division by zero

        # Select the action with the highest U value
        if u > cur_best:
            cur_best = u
            best_act = a

Balancing Exploration and Exploitation#

Unvisited nodes have a smaller denominator due to N(s, a) = 0, making the exploration term larger, encouraging the algorithm to explore new actions.
Q(s, a) reflects the current estimate of the action's value, representing exploitation.

Value Inversion#

From player $A$ 's perspective, obtaining a higher value for player $B$ means a lower value for player $A$ , and vice versa. Therefore, throughout the search and value evaluation process, ensuring that the value reflects the maximization of the current player's interests maintains perspective consistency.

In the code, this implementation is reflected in the following call:

v = -self.search(next_s)

Search Function#

def search(self, canonicalBoard):
    """
    Executes an MCTS search.

    Parameters:
    - canonicalBoard: The current player's board state (canonical form)

    Returns:
    - v: Value estimate for the current node
    """
    s = self.game.stringRepresentation(canonicalBoard)

    if s not in self.Es:
        self.Es[s] = self.game.getGameEnded(canonicalBoard, 1)
    if self.Es[s] is not None:
        # If the game has ended, return the result
        return self.Es[s]

    '''
    Valid Mask & Leaf Node Expansion
    '''

    valids = self.Vs[s]

    '''
    Use the PUCT formula to select the optimal action
    '''

    a = best_act
    next_s, next_player = self.game.getNextState(canonicalBoard, 1, a)
    next_s = self.game.getCanonicalForm(next_s, next_player)

    # The value of the next state is inverted
    v = -self.search(next_s)

    # Update Q value and visit count
    if (s, a) in self.Qsa:
        self.Qsa[(s, a)] = (self.Nsa[(s, a)] * self.Qsa[(s, a)] + v) / (self.Nsa[(s, a)] + 1)
        self.Nsa[(s, a)] += 1
    else:
        self.Qsa[(s, a)] = v
        self.Nsa[(s, a)] = 1

    self.Ns[s] += 1
    return v

Through recursive deep searches, it simulates future possibilities.
At leaf nodes, it uses neural network predictions to accelerate the search.
Since players alternate, the value of the next state is inverted.

Self-Play#

The Go algorithm that does not require human game data for training, only obtains data through self-play.

Self-play means that for each move, it executes several MCTS simulations to obtain an enhanced strategy $\pi(s,a)$ for choosing moves. The black and white players alternate until the game ends. Self-play generates a large amount of training data, helping the neural network learn better strategies and value estimates.

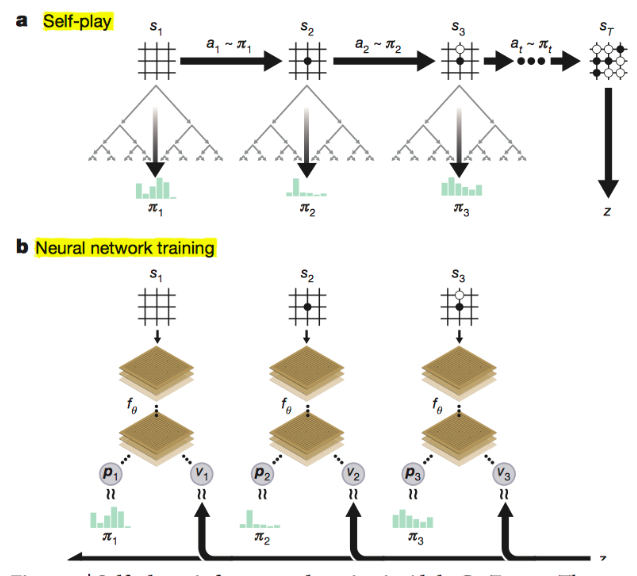
Implementing "Executing a Self-Play Game"#

First, let's look at the core function of Self-Play: executeEpisode, which is responsible for executing an entire game until the end and collecting training data.

def executeEpisode(self):
    """
    Executes a self-play game and returns a list of training samples.

    Returns:
        trainExamples: A list containing multiple (canonicalBoard, pi, v) tuples.
    """
    trainExamples = []
    board = self.game.getInitBoard()  # Initialize the board
    self.curPlayer = 1                # Current player (1 or -1)
    episodeStep = 0                   # Record the number of steps

    while True: # Until the game ends
        episodeStep += 1
        canonicalBoard = self.game.getCanonicalForm(board, self.curPlayer)

        temp = int(episodeStep < self.args.tempThreshold)  # Temperature parameter

        pi = self.mcts.getActionProb(canonicalBoard, temp=temp)  # Use MCTS to obtain the action probability distribution (policy)
        sym = self.game.getSymmetries(canonicalBoard, pi)        # Data augmentation (symmetry)
        for b, p in sym:
            trainExamples.append([b, self.curPlayer, p, None])

        action = np.random.choice(len(pi), p=pi)  # Choose an action according to the policy probabilities
        board, self.curPlayer = self.game.getNextState(board, self.curPlayer, action) # Execute the action, updating the board and current player.

        r = self.game.getGameEnded(board, self.curPlayer)  # Check if the game has ended
        if r is not None:
            # Assign final value to each training sample, +1 for the winning player, -1 for the losing player, 0 for a draw
            return [(x[0], x[2], r * ((-1)  (x[1] != self.curPlayer))) for x in trainExamples]

Temperature parameter: Controls the exploratory nature of the policy. Initially set to 1 to encourage exploration; later set to 0 to favor the optimal strategy leaning towards exploitation.
Data augmentation: In Gomoku, the rotation and flipping of the board do not change the essence of the game. Utilizing these symmetries generates equivalent boards and strategies, increasing training data to enhance the model's generalization ability.

If the game ends, training samples are generated based on the game records, returning trainExamples.

Main Loop of Self-Play#

Self-play is not just about executing a single game; we need to continuously perform self-play in multiple iterations to update the model.

def learn(self):
    """
    Conducts multiple iterations of self-play and model updates.
    """
    for i in range(1, self.args.numIters + 1):
        log.info(f"Starting Iter #{i} ...")
        # Store training samples from this iteration
        iterationTrainExamples = deque([], maxlen=self.args.maxlenOfQueue)

        # Perform the specified number of self-plays
        for _ in tqdm(range(self.args.numEps), desc="Self Play"):
            self.mcts = MCTS(self.game, self.nnet, self.args)  # Reset MCTS
            iterationTrainExamples += self.executeEpisode()

        # Save training samples
        self.trainExamplesHistory.append(iterationTrainExamples)

        # Maintain a fixed-length history of training samples
        if len(self.trainExamplesHistory) > self.args.numItersForTrainExamplesHistory:
            log.warning(f"Removing the oldest entry in trainExamples.")
            self.trainExamplesHistory.pop(0)

        # Merge and shuffle all training samples
        trainExamples = []
        for e in self.trainExamplesHistory:
            trainExamples.extend(e)
        shuffle(trainExamples)

        # Train the neural network
        self.nnet.save_checkpoint(folder=self.args.checkpoint, filename="temp.pth.tar")
        self.pnet.load_checkpoint(folder=self.args.checkpoint, filename="temp.pth.tar")
        pmcts = MCTS(self.game, self.pnet, self.args)

        self.nnet.train(trainExamples)
        nmcts = MCTS(self.game, self.nnet, self.args)

If the history length exceeds the set threshold, the oldest sample is removed to ensure the model does not overfit to old data.
After collecting enough training data, the model is trained using self.nnet.train(trainExamples).

Filtering Mechanism#

To ensure that the model's playing strength continuously improves, AlphaGo Zero introduces a filtering mechanism for new and old model matches:

After each training round, the new model is pitted against the old model.
- If the new model's win rate exceeds a set threshold (e.g., 55%), the new model is accepted, and the self-play continues into the next round; otherwise, the old model's weights are restored to continue generating data and training based on the old model, avoiding meaningless degradation and overfitting issues.

        # Evaluate the new model
        log.info("PITTING AGAINST PREVIOUS VERSION")
        arena = game.Arena(lambda x: np.argmax(pmcts.getActionProb(x, temp=0)),
                           lambda x: np.argmax(nmcts.getActionProb(x, temp=0)),
                           self.game)
        pwins, nwins, draws = arena.playGames(self.args.arenaCompare)

        log.info(f"NEW/PREV WINS : {nwins} / {pwins} ; DRAWS : {draws}")
        if pwins + nwins == 0 or float(nwins) / (pwins + nwins) < self.args.updateThreshold:
            log.info("REJECTING NEW MODEL")
            self.nnet.load_checkpoint(folder=self.args.checkpoint, filename="temp.pth.tar")
        else:
            log.info("ACCEPTING NEW MODEL")
            self.nnet.save_checkpoint(folder=self.args.checkpoint, filename="best.pth.tar")

Obtaining Strategy from MCTS#

During self-play, we use MCTS to select actions. The getActionProb function retrieves the probability distribution of actions from MCTS.

def getActionProb(self, canonicalBoard, temp=1):
    """
    Executes multiple MCTS searches and returns the probability distribution of actions.

    Parameters:
        canonicalBoard: The current normalized board state
        temp: Temperature parameter

    Returns:
        probs: Probability distribution of actions
    """
    # Perform the specified number of MCTS searches
    for _ in range(self.args.numMCTSSims):
        self.search(canonicalBoard) 

    s = self.game.stringRepresentation(canonicalBoard)
    # Record the number of times each action has been visited N(s, a)
    counts = [self.Nsa[(s, a)] if (s, a) in self.Nsa else 0 
              for a in range(self.game.getActionSize())]

    if temp == 0:
        bestAs = np.array(np.argwhere(counts == np.max(counts))).flatten()
        bestA = np.random.choice(bestAs)
        probs = [0] * len(counts)
        probs[bestA] = 1
        return probs

    counts = [x  (1. / temp) for x in counts]
    counts_sum = float(sum(counts))
    probs = [x / counts_sum for x in counts]
    return probs

The visit counts N(s, a) reflect MCTS's confidence in actions.

Calculating policy probabilities:

When temp = 0:
- Select the action with the highest visit count, probability 1.
- Ensures the policy is deterministic, typically used in the later stages of the game or evaluation phase.
When temp > 0:
- The visit counts undergo temperature transformation: counts = [x (1. / temp) for x in counts].
- Higher temperatures lead to a policy closer to a uniform distribution, enhancing exploration.

Training Process#

MCTS simulation times: 400, cpuct: 1.0, training for 50 rounds:

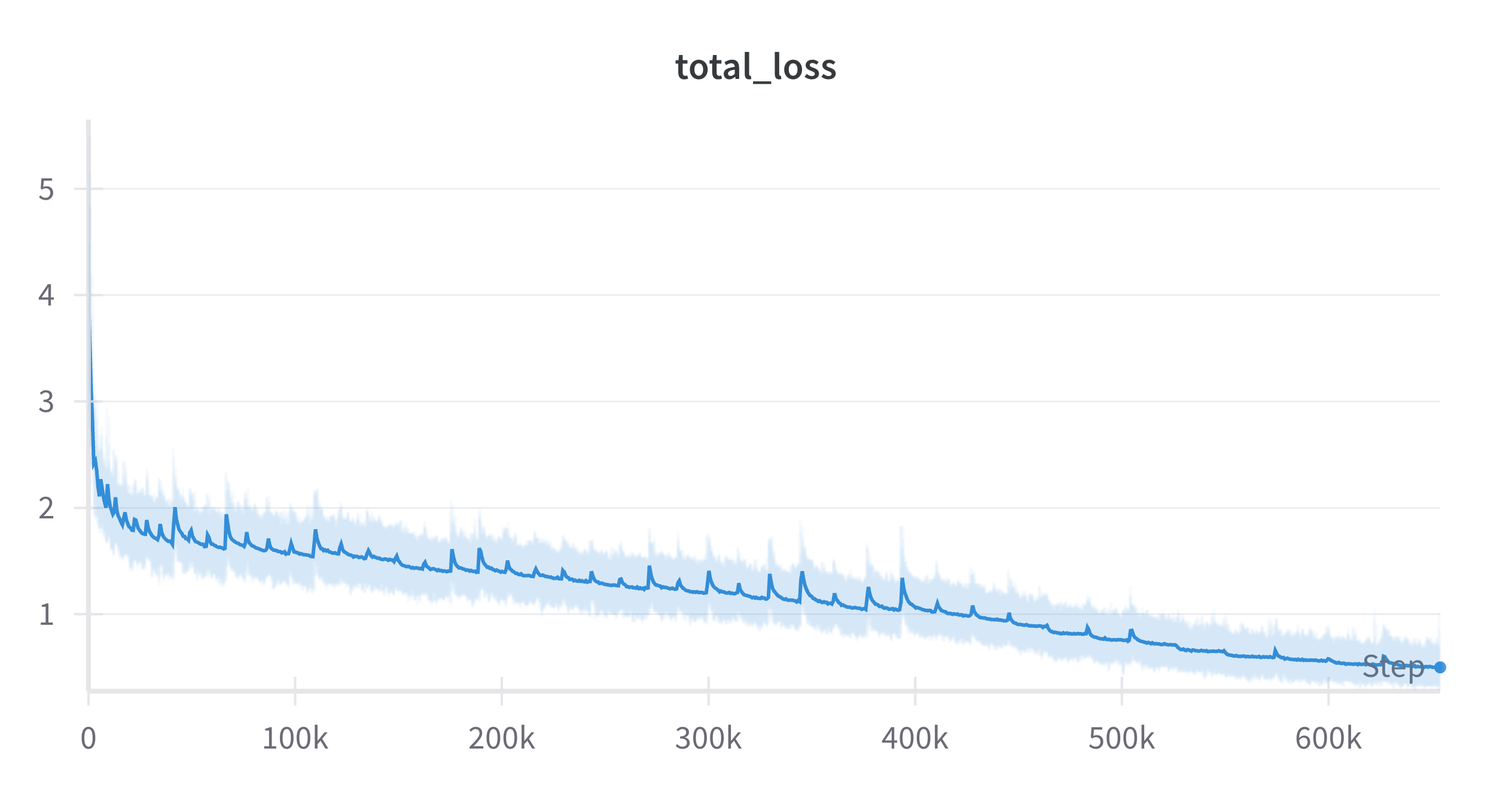
At this point, the model has learned the rules of Gomoku and reached a beginner-level AI, allowing you to sneak a win at the edge of the board.

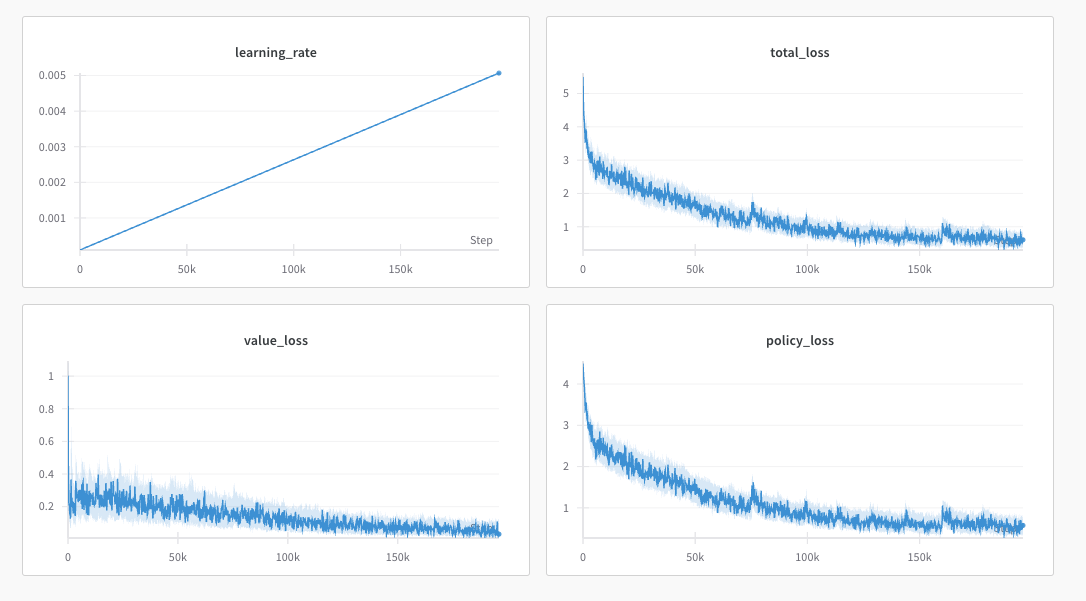
Adding 1cycle Learning Rate Adjustment#

Dynamically adjusting the learning rate can improve the model's convergence speed and generalization ability.

First phase (first half of the cycle): The learning rate gradually increases from the minimum value ( $1.0 \times 10^{-4}$ ) to the maximum value ( $1.0 \times 10^{-2}$ ).
Second phase (second half of the cycle): The learning rate gradually decreases back to the minimum value.

class NNetWrapper:
    def __init__(self, game, args):
        ...
        self.optimizer = optim.Adam(self.nnet.parameters(), lr=args.max_lr)
        
        # 1cycle learning rate parameters
        self.total_steps = args.numIters * args.epochs * (args.maxlenOfQueue // args.batch_size)
        self.current_step = 0

    def get_learning_rate(self):
        """Implement 1cycle learning rate strategy"""
        if self.current_step >= self.total_steps:
            return self.args.min_lr
        
        half_cycle = self.total_steps // 2
        
        if self.current_step <= half_cycle:
            # First phase: Increase from min_lr to max_lr
            phase = self.current_step / half_cycle
            lr = self.args.min_lr + (self.args.max_lr - self.args.min_lr) * phase
        else:
            # Second phase: Decrease from max_lr to min_lr
            phase = (self.current_step - half_cycle) / half_cycle
            lr = self.args.max_lr - (self.args.max_lr - self.args.min_lr) * phase
        
        return lr

Adding Gradient Clipping#

You can review PPO

To prevent gradient explosion and stabilize the training process, we add gradient clipping after backpropagation.
Assuming the gradient vector of a parameter is $\mathbf{g}$ , with its current L2 norm being $\|\mathbf{g}\|$ :

If $\|\mathbf{g}\| \leq 1.0$ , then $\mathbf{g}$ remains unchanged.
If $\|\mathbf{g}\| > 1.0$ , then $\mathbf{g}$ is scaled to $\frac{1.0}{\|\mathbf{g}\|} \cdot \mathbf{g}$ .

This ensures that:

\|\frac{1.0}{\|\mathbf{g}\|} \cdot \mathbf{g}\| = 1.0

def train(self, examples):
    ...
    for epoch in range(self.args.epochs):
        ...
        for _ in t:
            ...
            # Calculate loss and backpropagate
            total_loss.backward()

            # Gradient clipping
            if self.args.grad_clip:
                torch.nn.utils.clip_grad_norm_(self.nnet.parameters(), self.args.grad_clip)

            # Update parameters
            self.optimizer.step()
            ...

Gradient clipping limits the norm of the gradient to a specified threshold, preventing excessively large gradients from causing instability in training. By clipping gradients before each parameter update, we ensure the robustness of the training process and accelerate the model's convergence.

Conclusion#

The final code and demo can be found in the repository below, and the model weights can be found in the huggingface link repository in the documentation.

Nagi-ovo/alphazero-gomoku

Python00

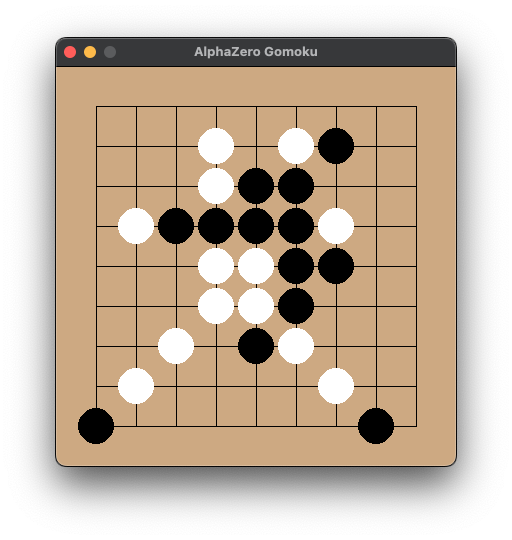
After making these improvements, the number of MCTS simulations was increased to 2000, and cpuct: 4.0 was set to increase exploration tendency, training for 22 rounds (running on a single 3090 Ti for 4 days). At this point, our model gradually upgraded to an intermediate difficulty (under the setting of 50 MCTS simulations, the early pressure is acceptable, but in the mid-to-late stages, one may overlook the opponent's winning points).

If increasing the number of MCTS simulations during inference can elevate it to the level of a difficult AI, feel free to try and see if you can win.