
学习策略梯度方法的基本原理和实现,了解如何通过直接优化策略来训练强化学习智能体。
Policy Gradient 入门学习
本文是对学习 Andrej Karpathy 的 Deep RL Bootcamp 及其博客的记录,博客链接:Deep Reinforcement Learning: Pong from Pixels
RL 的进展并不主要由新奇惊人的想法推动:
2012 年的 AlexNet 主要是对 1990 年代 ConvNets 的扩展(更深更宽)。 2013 年关于 ATARI 游戏的深度 Q 学习论文,其实是对一种标准算法的实现(即带有函数逼近的 Q 学习,Sutton 1998),其中函数逼近器恰好是 ConvNet。AlphaGo 使用了策略梯度结合蒙特卡洛树搜索(MCTS),这些也都是标准组件。当然,要让这些算法有效运行需要大量的技巧和耐心,并且在旧算法基础上开发了许多巧妙的改进,但粗略来看,近期进展的主要驱动力并非算法本身,而是(与计算机视觉类似)计算能力、数据和基础设施。 ——Andrej Karpahy
ATARI Pong
Pong 是马尔可夫决策过程(MDP)的一个特例:一个图,其中每个节点代表一个特定的游戏状态,每条边代表一个可能的(通常是概率性的)转移。每条边还赋予一个奖励,目标是计算出在任何状态下采取最优行动以最大化奖励的方法。
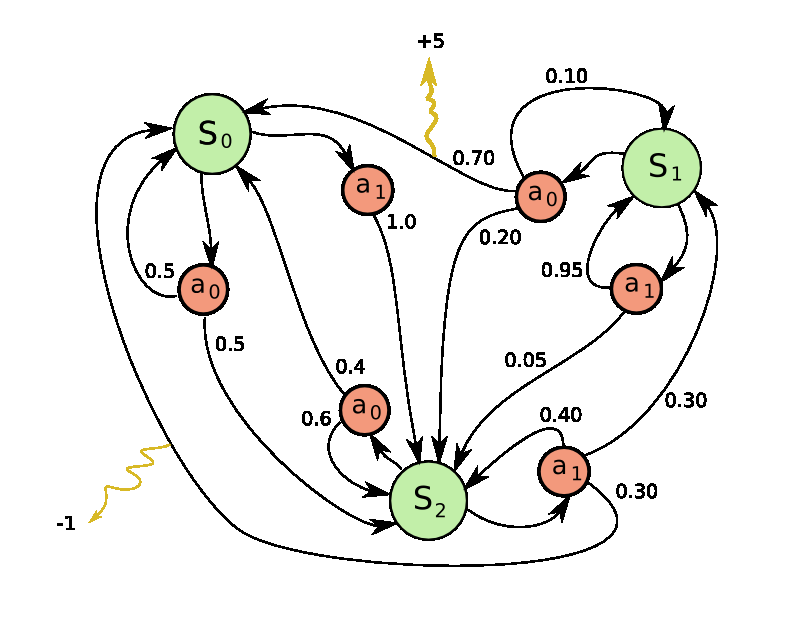
马尔可夫决策过程(Markov Decision Process, MDP)是一个数学框架,用于在不确定性环境下进行决策。MDP 通过考虑当前状态、可能的行动、状态转移概率和奖励函数,帮助决策者在面对随机因素时做出最佳决策。
游戏原理
我们收到图像帧(表示像素值的 0-255 的字节数组),以此决定是否将球拍向上或向下移动(二元选择)。做出选择后,游戏模拟器执行此操作并给予我们一个奖励:球越过对手(赢球)奖励为 +1,未击中球 -1,否则奖励为 0,我们的目标就是移动球拍以获得尽可能的多的奖励。
在解决方案的探讨中,会尽量减少对该游戏的假设,仅作为玩具案例来学习。
策略梯度
Policy Gradient 算法因其端到端特性而备受青睐:它有明确的策略和原则性方法,直接优化预期奖励
Policy Network
定义一个 Agent 的策略网络,它接收游戏状态,决定应该采取的决策(向上或向下)。这里使用一个两层的 nn,接收原始图像像素(210×160×3=100,800 210\times160\times3=100,800),并生成一个表示向上移动概率的数。通常使用随机策略而不是确定性决策,即每次迭代时从概率分布中进行采样(即抛一枚有偏的硬币,p p & (1−p) (1-p) )以获取实际的移动(允许智能体有时选择次优动作,可能发现更好的策略。)。
h = np.dot(W1, x) # 计算隐藏层神经元的激活 (权重矩阵点乘输入)
h[h < 0] = 0 # ReLU:小于 0 的值置为 0,即 max(0, h)
logp = np.dot(W2, h) # 计算向上移动的对数概率,W2 是隐藏层到输出层的权重矩阵
# 用 Sigmoid 将 log 概率转换为向上的概率值(0, 1)
p = 1.0 / (1.0 + np.exp(-logp)) 直观上,隐藏层中的神经元(权重沿W1的行排列)可以检测各种游戏场景,而W2中的权重则可以决定在每种情况下我们应该向上还是向下移动。初始情况下,随机初始化的参数的效果是玩家在原地抽搐,目标即为找到精通游戏的W1、W2。
预处理
理想情况下,我们希望向神经网络中至少输入 2 帧图像(以检测到运动)。为了简化操作,我们可以对输入图像做预处理,即输入当前帧与上一帧的差值。
Credit Assignment Problem
到这里可以想象,可能在经过数百个时间步后才得到非零奖励,但这时我们也不知道是哪一步起了作用,是上一步,第 10 帧和第 90 帧还是那几个参数?
这便是 RL 中的信用分配问题(Credit Assignment Problem, CAP)。在我们的场景下,得到 +1 奖励的原因是我们碰巧把球弹出了良好的轨迹并超过了对方的拍子,但这一个动作是得到奖励前的许多帧之前做的。也就是说,在某一步之后,我们采取的所有动作都对获得奖励没有帮助。
Supervised Learning
在深入策略提督解决方案前,先回顾一下与强化学习很像的监督学习。监督学习的目标是通过反向传播调整参数,使模型越来越精确地预测出正确的类别。
模型接收图片输入,输出类别的概率。例如,网络给出类别 UP 和 DOWN 的对数概率 ,对应的实际概率为 30% 和 70%。我们知道正确的标签(例如 UP),因此优化目标是最大化这个标签的对数概率。我们会计算 UP 的对数概率的梯度,并使用反向传播调整网络的参数。
通过计算 得到梯度,这个梯度会告诉我们如何调整每个参数,使得模型更倾向于预测 UP。
- 若某个参数的梯度是 -2.1,表示我们可以通过减少该参数(比如减少 0.001),使得 UP 的对数概率下降 。
- 完成参数更新后,网络会在类似情况下稍微更倾向于预测 UP。
Policy Gradient
但是在强化学习场景中,我们没有正确的标签,这就是 PG 的用武之地了:
- 初始阶段:模型计算出 UP 的概率为 30% 和 DOWN 的概率为 70%(),我们从这个分布中随机采样一个动作,比如选择 DOWN,并执行。
- 梯度计算:我们可以像监督学习一样,立刻对所选动作(DOWN)的对数概率计算梯度。但此时我们还不知道这个动作是否是好动作。
- 等待反馈:可以等待游戏结束后,获得奖励。例如在 Pong 中,如果我们输了游戏,得到奖励 -1,则将这个 -1 作为 DOWN 动作的梯度进行反向传播。
- 优化效果:在这个例子中,DOWN 导致了失败,梯度会使网络减少未来对 DOWN 动作的选择。
因此,策略梯度方法根据延迟奖励来调整策略,使得模型在未来更可能采取成功的动作。
Training Protocol
完整的训练流程如下:
- 用随机的
W1、W2初始化策略网络 - 进行 100 场 Pong 游戏(策略回放,rollouts)
假设每场比赛有 200 帧,总共做了 20,000 次向上或向下的决策。我们可以为每次决策计算参数梯度,这告诉我们如何调整模型以鼓励特定状态下的决策。
- 学习更新:
- 假设赢了其中的 12 场比赛,则在这 12 场比赛中的 2400 次决策会被正向更新(梯度填入 +1.0),鼓励这些决策。
- 由于输了另外 88 场比赛,则在这 88 场比赛中的 17600 次决策会被负向更新,不鼓励这些决策。
网络会略微增加有效动作的概率,并略微减少无效动作的概率。
- 我们使用这个略微改进的策略再玩 100 局游戏,重复 2,3 的过程,不断优化策略。
[!Karpathy’s summary] Policy Gradients: Run a policy for a while. See what actions led to high rewards. Increase their probability. 策略梯度:运行策略一段时间。观察哪些行动带来了高回报。增加它们的概率。

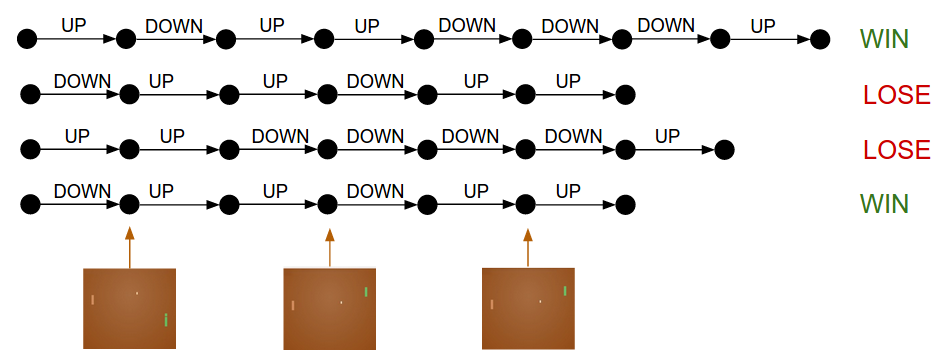
如图,每个黑色圈代表游戏状态,每个箭头表示状态转移,并附上采样的动作。使用 PG 时,我们选取赢的两场比赛,轻微地鼓励该回合中的每一个动作,反之则抑制。
那么问题来了,假设我们在第 50 帧做了“将球弹回”的正确决策,但最终结果是在第 150 帧错过了球而失败,根据上面的训练规则,该回合的每一个动作都将被抑制,那这样会打击到我们第 50 帧所做的正确决策吗?
答案是会的,然而当我们考虑到整个游戏样本空间中成千上万,甚至上百万的比赛过程时,正确的决策回让我们在未来更有可能获胜,因此平均来看,我们的最终策略会做出正确的行动。
策略梯度与监督学习的联系
策略梯度法其实和监督学习类似,只是:
- 我们用模型采样到的动作作为“标签”。
- 我们根据动作的好坏(奖励或惩罚)调整损失函数的权重。
在标准的监督学习中,目标是最大化每个训练样本的对数概率 其中 是输入(图片), 是正确标签(图片的类别)。
在强化学习中,我们没有正确标签 。所以,我们把策略模型采样到的动作(例如向上或向下)作为“假标签”。我们根据最终结果(例如赢或输)来调整每个样本的损失权重,用来增加有效动作的概率,减少无效动作的概率。
因此在强化学习中,损失函数会看起来像是 其中:
- 是我们模型采样到的动作(即“假标签”)。
- 是优势值,用来衡量这个动作最终的好坏结果。
- 如果动作最终导致了胜利,;
- 如果导致了失败,。
因此,强化学习可以看作是 在不断变化的数据集(回合) 上进行的监督学习,而这些数据集是从不同的游戏或情景中采样出来的,并且我们根据结果来调整每个样本的损失大小。
General Advantage Function
我们先前是基于是否赢球来判断每个行动的好坏,而在更一般的 RL 环境中,我们会在每个时间步获得某种即时奖励 ,例如游戏中的得分、环境中的反馈等。
Discounted Reward
常见的方式是使用 折扣奖励(Discounted Reward) 来计算某个动作之后的累计回报。折扣奖励的公式为:
- 是折扣因子,范围在 0 到 1 之间(例如 0.99),用于降低未来奖励的影响。
- 从当前时间 开始,未来每个时间步的奖励 都按距离当前时刻的远近乘以折扣,离得越远的奖励被减弱得越多。
Normalize Returns
当我们为 20,000 个动作(例如 100 局 Pong 游戏中的所有动作)计算完 后,将这些返回值进行标准化是一种常见的做法。如减去均值并除以标准差来实现:
标准化可以平衡鼓励和惩罚的动作比例,确保在一个 batch 中大约有一半的动作被鼓励,另一半被惩罚。从数学上来讲,这可以解释为控制策略梯度估计方差的一种方法。减少方差意味着梯度更新更加稳定,模型更容易收敛。
PG 推导
策略梯度是一种更一般的评分函数梯度估计器的特例。我们考虑以下表达式:
其中:
- 是标量值评分函数 (在强化学习中通常是奖励函数或优势函数)
- 是由参数 参数化的概率分布 (在强化学习中通常是策略网络)
目标:找出如何调整分布 (通过改变其参数 ) 来增加其样本的得分。
[! 理解这里的 trick] 对数函数求导的基本性质:
用 来表示对 的梯度:
[!OpenAI Spinning Up 的版本:]
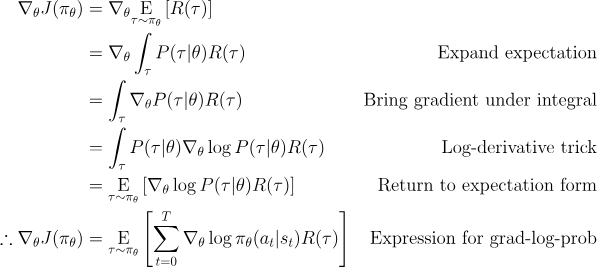
这是一种期望,意味着我们可以用样本均值来估计它。如果我们收集一组轨迹 ,其中每条轨迹是通过让智能体在环境中使用策略 行动获得的,那么策略梯度可以用以下方法估计: 其中 表示 中的轨迹数量(此处为 )。 这个最后的表达式是我们所期望的可计算表达式的最简版本。假设我们已经以某种方式表示了我们的策略,使得我们能够计算 ,并且如果我们能够在环境中运行该策略以收集轨迹数据集,我们就可以计算策略梯度并采取更新步骤。
Practice in GYM
模型初始化
H = 200 # 隐藏层神经元数量
batch_size = 10 # 每多少个 episode 更新一次参数
learning_rate = 1e-4
gamma = 0.99 # 奖励折扣因子
# 模型初始化
D = 80 * 80 # 输入维度:80x80 网格
model = {}
model['W1'] = np.random.randn(H,D) / np.sqrt(D) # "Xavier" 初始化
model['W2'] = np.random.randn(H) / np.sqrt(H)辅助函数
def prepro(I):
""" 将 210x160x3 的 uint8 帧预处理成 6400 (80x80) 的 1D 浮点向量 """
I = I[35:195] # 裁剪
I = I[::2,::2,0] # 降采样
I[I == 144] = 0 # 擦除背景
I[I == 109] = 0 # 擦除背景
I[I != 0] = 1 # 其他(球拍,球)设为 1
return I.astype(np.float64).ravel()
def discount_rewards(r):
""" 计算折扣奖励 """
discounted_r = np.zeros_like(r)
running_add = 0
for t in reversed(range(0, r.size)):
if r[t] != 0: running_add = 0 # 重置和,因为这是游戏边界(Pong 特有)
running_add = running_add * gamma + r[t]
discounted_r[t] = running_add
return discounted_r策略网络
def policy_forward(x):
h = np.dot(model['W1'], x)
h[h<0] = 0 # ReLU 非线性
logp = np.dot(model['W2'], h)
p = sigmoid(logp)
return p, h # 返回采取动作 2 的概率,和隐藏状态
def policy_backward(eph, epdlogp):
""" 反向传播 """
dW2 = np.dot(eph.T, epdlogp).ravel()
dh = np.outer(epdlogp, model['W2'])
dh[eph <= 0] = 0 # 反向传播 ReLU
dW1 = np.dot(dh.T, epx)
return {'W1':dW1, 'W2':dW2}实现策略网络的 forward & backward
主循环
while True:
# 预处理观察
cur_x = prepro(observation)
x = cur_x - prev_x if prev_x is not None else np.zeros(D)
prev_x = cur_x
# 前向传播并采样动作
aprob, h = policy_forward(x)
action = 2 if np.random.uniform() < aprob else 3
# 记录中间状态
xs.append(x) # 观察
hs.append(h) # 隐藏状态
y = 1 if action == 2 else 0 # "假标签"
dlogps.append(y - aprob) # 鼓励所采取动作的梯度
# 执行动作
observation, reward, done, info = env.step(action)
reward_sum += reward
drs.append(reward) # 记录奖励Episode 结束时处理
if done:
episode_number += 1
# 堆叠这个 episode 的所有输入、隐藏状态、动作梯度和奖励
epx = np.vstack(xs)
eph = np.vstack(hs)
epdlogp = np.vstack(dlogps)
epr = np.vstack(drs)
xs,hs,dlogps,drs = [],[],[],[] # 重置数组内存
# 计算折扣奖励
discounted_epr = discount_rewards(epr)
# 标准化奖励
discounted_epr -= np.mean(discounted_epr)
discounted_epr /= np.std(discounted_epr)
epdlogp *= discounted_epr # 用优势调整梯度(策略梯度的核心)
grad = policy_backward(eph, epdlogp)
for k in model: grad_buffer[k] += grad[k] # 在 batch 中累积梯度每个 episode 结束时计算策略梯度并累积到梯度缓冲中。
参数更新
grad_buffer = { k : np.zeros_like(v) for k,v in model.items() } # update buffers that add up gradients over a batch
rmsprop_cache = { k : np.zeros_like(v) for k,v in model.items() } # rmsprop memory if episode_number % batch_size == 0:
for k,v in model.items():
g = grad_buffer[k] # 梯度
rmsprop_cache[k] = decay_rate * rmsprop_cache[k] + (1 - decay_rate) * g**2
model[k] += learning_rate * g / (np.sqrt(rmsprop_cache[k]) + 1e-5)
grad_buffer[k] = np.zeros_like(v) # 重置 batch 梯度缓冲使用 RMSProp 算法更新模型参数。
AK 的反思
对于人类,我们会说“你控制一个可以上下移动的球拍,你的任务是将球反弹过 AI 对手”,而在标准强化学习问题中,我们通过与环境交互来假设一个任意的奖励函数。人类玩家会带入大量先验知识(如球轨迹遵循物理定律,AI 对手可能的移动策略这样的直觉心理学),并且需要时刻看到正常的游戏画面。但对于策略梯度解决方案,甚至如果对获取帧的像素随机排列,使用全连接网络的策略梯度甚至都察觉不到有差异。
因此,策略梯度是一种暴力破解方法,发现正确的行动并内化为策略。
策略梯度能在很多游戏中轻松击败人类。特别是那些需要频繁奖励信号、精确操作、快速反应且不需要太多长期规划的游戏,因为这些短期奖励与行动之间的关联可以被该方法轻易”察觉”,并通过策略精心完善执行。在 Pong 游戏训练后期的结果就可以看出:Agent 等球快到了,就迅速移动接住球,然后以快速且高垂直速度发射球。在许多 ATARI 游戏中,深度 Q 学习正是以这种方式彻底超越了人类的基础表现——例如弹球、打砖块等。