Nagi-ovo

本文主要以該視頻的教學邏輯為主線，結合講解內容進行整理和闡述，如有錯誤歡迎在評論區糾正！

直覺部分#

理論支持#

Deep Unsupervised Learning using Nonequilibrium Thermodynamics

這篇論文奠定了擴散模型的理論基礎。作者提出了一種基於非平衡熱力學的生成模型，通過逐步添加和去除噪聲來實現數據生成。這為後續的擴散模型研究提供了重要的理論支持。

我們對圖像應用大量噪聲，然後用神經網絡去噪。如果這個神經網絡學得很好，那可以從完全隨機的噪聲開始最終得到我們訓練數據中的圖像。

Forward Diffusion Process:#

迭代地對圖像施加噪聲，步驟足夠多時圖像會完全變成噪聲，使用正態分布作為噪聲源：

Reverse Diffusion Process#

從純粹的噪聲到圖像，涉及一個學習一步步去噪的神經網絡。

為什麼是逐漸去噪？作者在論文中提到 “一步直接完成去噪” 的結果很糟糕。

那麼這個網絡是什麼樣的？它又要預測什麼？

算法改進#

Denoising Diffusion Probabilistic Models

這篇論文提出了去噪擴散概率模型（DDPM），顯著提高了擴散模型的生成質量和效率。通過引入簡單的去噪網絡和優化的訓練策略，DDPM 成為了擴散模型領域的一個重要里程碑。

作者討論了神經網絡可以預測的三種目標：

1. 預測每個時間步的噪聲均值 (predict the mean of the noise at each timestep)

   • 即預測條件分布 $p(x_{t-1}|x_t)$ 的均值
   • 方差是 fixed 的，不可學習

2. 預測原始圖像 (predict $x_0$ directly)

   • 直接預測原始、未被污染的圖像
   • 實驗證明這種方式效果較差

3. 預測添加的噪聲 (predict the added noise)

   • 預測在正向過程中添加的噪聲 $ε$
   • 和第一種方法（預測噪聲均值）實際上是數學上等價的，只是參數化方式不同，它們可以通過簡單的變換相互轉換

論文最終選擇了預測噪聲（第三種方式）作為主要方法，因為這種方式訓練更穩定且效果更好

這裡每一步添加的噪聲量是不固定的，通過一個 Linear Schedule 來控制噪聲添加，防止訓練過程不穩定。

大概長下面這樣：

可以看到最後最後幾個時間步都接近完全噪聲了，信息很少，此外整體來看信息摧毀得太快了，因此 OpenAI 使用了 Cosine Schedule 解決了這兩個問題：

模型架構#

U-Net#

隨著這篇論文一起發表的是一個名叫 U-Net 的模型架構：

這個模型在中間有一個 Bottleneck（也就是參數量較小的層），用 Downsample-Block 和 Resnet-Block 來將輸入圖像投影到小分辨率，輸出時用 Upsample-Block 將其投影回初始尺寸。

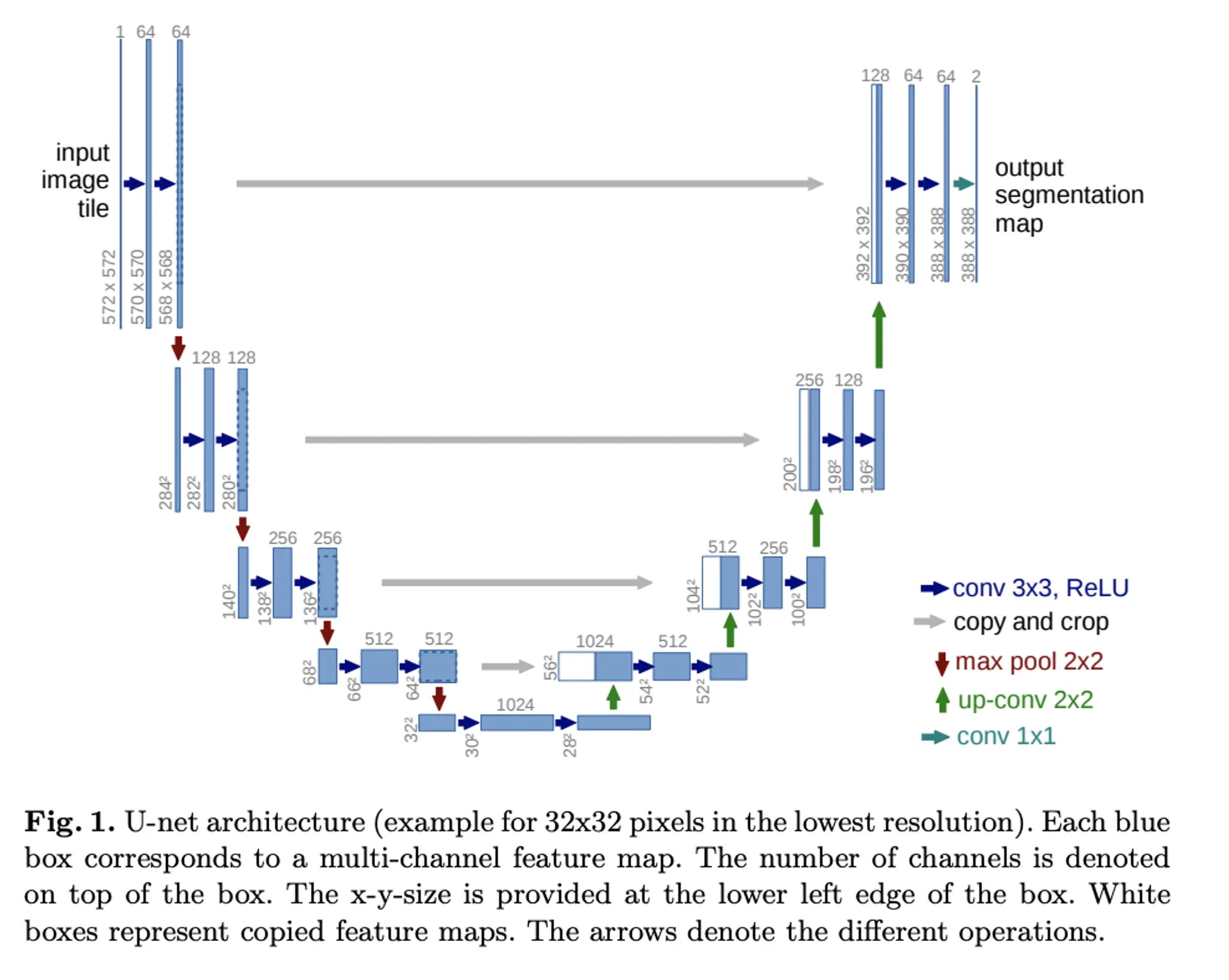
在某些分辨率下，作者加入了 Attention-Block 並在相同分辨率空間的層之間做 Skip-Connection。模型是被涉及為針對每一個時間步的，這是通過 Transformer 中的正弦位置編碼嵌入來實現的，嵌入被投影到每個 Residual-Block 中。模型還能結合 Schedule，在不同時間步中去除不同量的噪聲來提升生成效果，後面會詳細討論。

Bottleneck 和 Autoencoder#

Bottleneck（瓶頸層）的概念最初是在無監督學習方法 "自編碼器（Autoencoder）" 中提出並廣泛使用的。作為自編碼器架構中維度最低的隱藏層，它位於編碼器和解碼器之間，構成了網絡中最窄的部分，強制網絡學習數據的壓縮表示，最小化重建誤差並起到正則化作用：$\mathcal{L}_{\text{reconstruction}} = \|X - \text{Decoder}(\text{Encoder}(X))\|^2$

架構改進#

OpenAI 在他們的第二篇論文 Diffusion Models Beat GANs on Image Synthesis 中通過改進架構顯著改善了整體效果：

1. 增加網絡深度（更多層），減少寬度（每層的通道數）
2. 增加 Attention-Block 數量
3. 並擴大每個 Attention Block 中的 heads 數量
4. 引入 BigGAN 風格的 Residual Block 用於上採樣和下採樣
5. 引入 Adaptive Group Normalization (AdaGN)，通過條件信息（如時間步）來動態調整歸一化的參數
6. 用 Separate Classifier Guidance 幫助模型生成某類圖片

數學部分#

符號表#

• $X_t$ 代表在 $t$ 時間步的圖像，即 $X_0$ 是原始圖像。可以簡記 $t$ 越小噪聲越少：

• 噪聲的最終圖像是一個 isotropic（各方向相同） 的完全噪聲，記作 $X_T$，在最開始的研究中 $T=1000$，後續工作會將其減小很多：

• Forward Process：$q(x_t|x_{t-1})$，輸入$x_{t-1}$圖像輸出一張噪聲更多的圖像$X_t$：

• Backward Process：$p(x_{t-1}|x_t)$，輸入 $x_t$ 圖像用神經網絡輸出一個降噪的圖像 $x_t-1$：

正向過程#

其中，

• $\sqrt{1 - \beta_t} x_{t-1}$ 是分布的均值（mean）；$\beta_t$ 是 noise schedule 參數，範圍在 0 到 1 之間，配合$\sqrt{1 - \beta_t}$ 對噪聲完成縮放，隨著時間步增加而減小，表示保留的原始信號部分。

• $\beta_t I$ 是分布的協方差矩陣（covariance matrix），$I$ 是單位矩陣，表示協方差矩陣是對角的且各維度獨立，隨著時間步增加，添加的噪聲量增大。

現在我們只需要將這個步驟不斷迭代執行即可得到 1000 步後的結果，但其實這些可以一步完成。

Reparameterization Trick#

重參數化技巧在擴散模型和其他生成模型（如變分自編碼器，VAE）中非常重要。它的核心思想是將隨機變量的採樣過程轉化為一個確定性函數加上一個標準化的隨機變量。這種轉換使得模型可以通過梯度下降進行優化，因為它消除了採樣過程中的隨機性對梯度計算的影響。

這裡通過一個簡單的例子來解釋其意義

你要實現一個扔骰子可以有兩種方式，

• 第一種是隨機性在函數內部：

# 1. 直接掷骰子（隨機採樣）
def roll_dice():
    return random.randint(1, 6)

result = roll_dice()

• 第二種則是讓隨機性在函數外部，函數本身是確定性的：

# 2. 將隨機性分離出來
random_number = random.random()  # 生成0到1之間的隨機數

def transformed_dice(random_number):
    # 將0-1的隨機數映射到1-6
    return math.floor(random_number * 6) + 1

result = transformed_dice(random_number)

概率論中我們學過：如果 $X$ 是一個隨機變量，且 $X ∼ 𝒩(0,1)$，那麼有：$aX + b ∼ 𝒩(b, a²)$

因此對於正態分布 $\mathcal{N}(\mu, \sigma^2)$ 可以通過以下方式生成樣本：

其中 $\epsilon \sim \mathcal{N}(0, 1)$ 是標準正態分布。

那同理，在正態分布中，

• 不使用重參數化：

# 直接從目標正態分布採樣
x = np.random.normal(mu, sigma)

• 使用重參數化：

# 先從標準正態分布採樣
epsilon = np.random.normal(0, 1)
# 然後通過確定性變換得到目標分布
x = mu + sigma * epsilon

對應到模型訓練中涉及的梯度計算時，

不使用重參數化：

def sample_direct(mu, sigma):
    return np.random.normal(mu, sigma)

# 這種情況下很難計算關於mu和sigma的梯度
# 因為隨機採樣操作阻斷了梯度傳播

使用重參數化：

def sample_reparameterized(mu, sigma):
    epsilon = np.random.normal(0, 1)  # 梯度不需要通過這裡傳播
    return mu + sigma * epsilon        # 可以輕鬆計算mu和sigma的梯度

以 VAE（變分自編碼器）為例：

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        self.encoder = Encoder()  # 輸出mu和sigma
        self.decoder = Decoder()

    def reparameterize(self, mu, sigma):
        # 重參數化技巧
        epsilon = torch.randn_like(mu)  # 從標準正態分布採樣
        z = mu + sigma * epsilon        # 確定性變換
        return z

    def forward(self, x):
        # 編碼器輸出mu和sigma
        mu, sigma = self.encoder(x)
        
        # 使用重參數化採樣
        z = self.reparameterize(mu, sigma)
        
        # 解碼器重建輸入
        reconstruction = self.decoder(z)
        return reconstruction

吃貨視角的重參數化#

想像你在製作奶茶：

不使用重參數化：

• 直接製作一杯特定甜度的奶茶
• 如果不好喝，你不知道是糖放多了還是放少了

使用重參數化：

1. 先準備一杯標準濃度的糖水（$\epsilon$）
2. 然後通過調整糖水的量（$\mu$）和稀釋程度（$\sigma$）來達到目標甜度
3. 如果不好喝，你可以清楚地知道是糖水量還是稀釋程度需要調整（參數可優化）

總之，經過重參數化：

• 梯度可以通過確定性變換傳播
• 參數可以通過梯度下降優化
• 隨機性被隔離，不影響梯度計算

正向數學推導#

從 $x_{t-1}$ 到 $x_t$ 的轉移：

• 給定 $x_{t-1}$，我們希望生成 $x_t$。
• 對 $q(x_t \mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)$ 使用重新參數化技巧，

可將 $x_t$ 表示為 $x_{t-1}$ 的確定性變換加上噪聲項：

• 這裡，$\sqrt{1 - \beta_t} x_{t-1}$ 是均值部分，$\sqrt{\beta_t} \epsilon$ 是噪聲部分。由於 $\epsilon$ 是標準正態分布的樣本，與模型參數無關，因此在反向傳播時，梯度只需考慮 $\sqrt{1 - \beta_t}$ 和 $\sqrt{\beta_t}$ 對應的參數。這使得模型可以通過梯度下降進行有效優化。

我們用 $\alpha_t$ 簡化記法 & 記錄其乘積的累計：

可得：

計算兩步轉移：從 $x_{t-2}$ 到 $x_t$

因為 $\epsilon_{t-1}$ 和 $\epsilon_t$ 是獨立的標準正態分布，合併噪聲部分為一個新的噪聲項 $\epsilon \sim \mathcal{N}(0, I)$：

同理：

完整推導流程如下：

逆向數學推導#

由於方差是固定的而不需要去學習 (見 1.3)，所以我們只需要神經網絡去預測均值：

我們的最終目標是預測兩個時間步中的噪聲，現在從損失函數開始分析：

但是這個負對數似然中，$x_0$的概率依賴前面的所有其它時間步。我們可以學習一個逼近這些條件概率的模型作為解決方案，這裡就需要用到 Varational Lower Bound (變分下界) 來得到一個更好計算的公式。

變分下界#

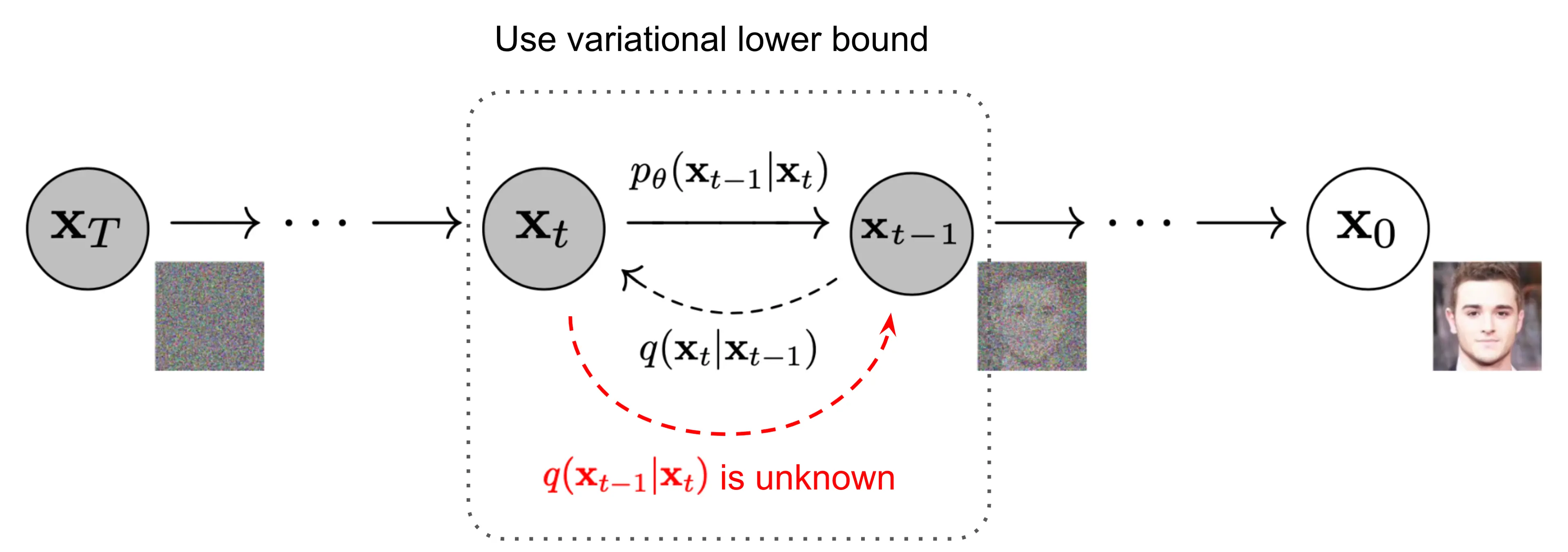
假設我們有一個無法計算的函數$f(x)$，在我們的場景中是負對數似然，我們可以找一個始終滿足 $g(x) \leq f(x)$ 的可計算函數 $g(x)$ ，那麼優化 $g(x)$ 也可以讓 $f(x)$ 增加：

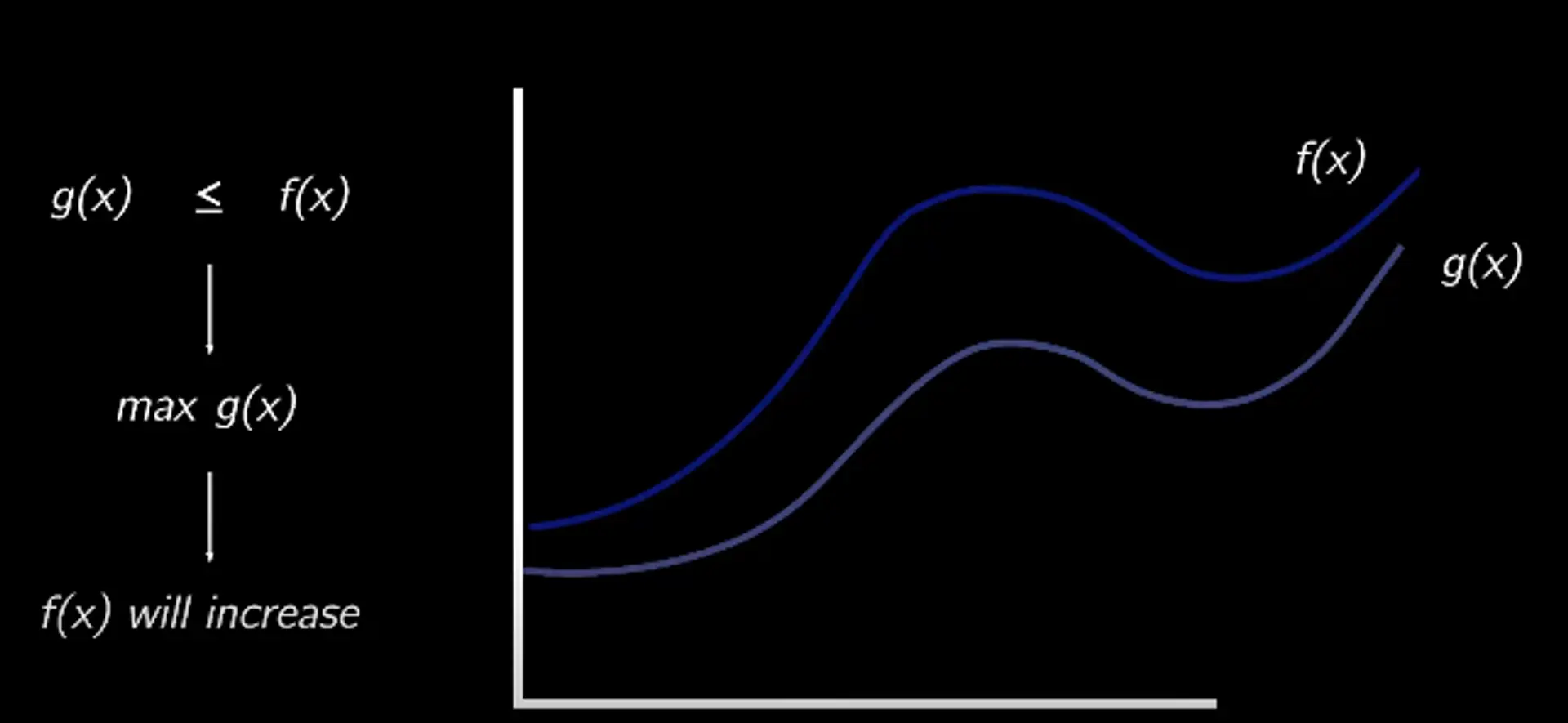
我們這裡通過減去 KL 散度來保證這點，KL 散度是衡量兩個分布相似度的指標，始終非負：

減去一個始終非負的項可以保證結果始終小於原始函數，這裡用 “+” 是因為我們想要最小化損失，所以加上後始終保證原始的負對數似然大：

這種形式下，因為負對數似然還在，下界仍然是不可計算的，我們需要得到一個更好的表達。首先將 KL 散度重寫為兩個項的對數比：

再對其分母應用貝葉斯法則：

上式的分子部分 $p_\theta(x_0 \mid x_{1:T}) p_\theta(x_{1:T})$ 實際上是聯合概率 $p_\theta(x_0, x_{1:T})$，因為：

通常， $p_\theta(x_{0:T})$ 表示 $x_0$ 和所有中間步驟 $x_{1:T}$ 的聯合概率，即：

代入有：

即按照下圖中的流程得到最後形式：

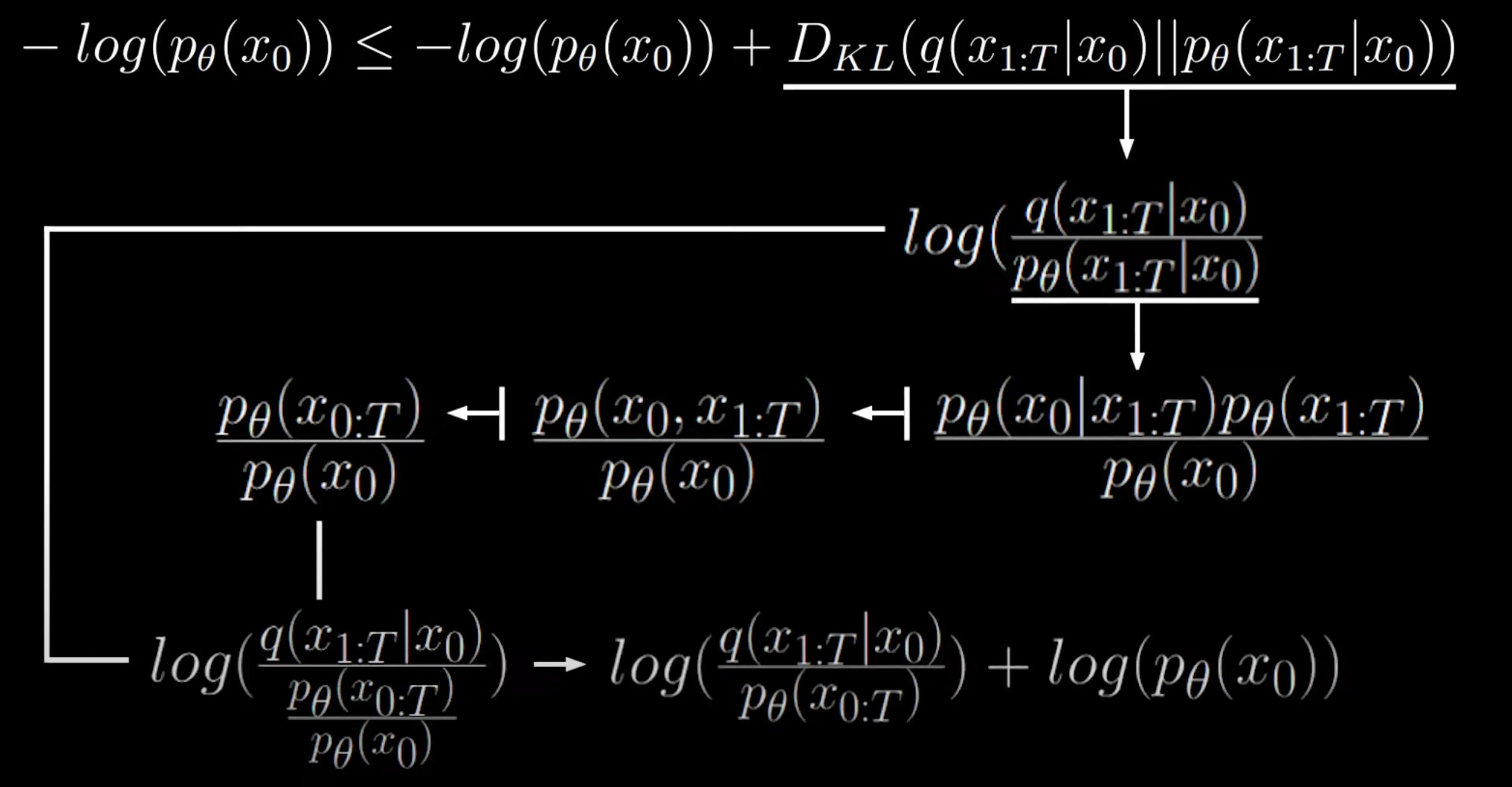
豁然開朗，煩人的兩項消掉了：

這樣就得到了可以最小化的下限，並且式中的內容都是已知的：

• 分子是正向過程的聯合概率分布：$q(x_{1:T} \mid x_0)=\prod_{t=1}^T q(x_t \mid x_{t-1})$；
• 分母是逆向過程的聯合概率分布：$p_\theta (x_{0:T})=p(x_T) \prod_{t=1}^T p_\theta(x_{t-1} \mid x_t)$

為了讓其有解析解，還需要幾個額外的重組步驟：

根據貝葉斯法則重寫 sum 項的分子：$q(x_t \mid x_{t-1})=\frac{q(x_{t-1}\mid x_t)q(x_t)}{q(x_{t-1})}$

但這又回到了前面，這些項都是需要估計全部樣本導致 high variance，如給出下圖所示的 $x_t$，你很難確定上個狀態是什麼樣的：

改進思路則為通過直接條件化於原始數據 $x_0$：

這樣同時給出無噪聲的圖像，侯選的 $x_{t-1}$ 就少了，方差會減小：

代入回原式：

展開第二個 sum 項，可以發現大部分項都被化簡掉了：

對最後兩項應用 log rules 可以化簡一些項：

再將化簡後的第一項移到前面，合併成一個對數得到最終解析形式：

這個形式的第一項是可以忽略的，因為 $q$ 沒有可學習參數，只是加噪聲的正向過程，會收斂為正態分布，而 $p(x_T)$ 只是從高斯分布中隨機採樣的噪聲，因此可以確定該項 KL 散度會很小。

剩余兩項的推導結果如下（過程省略，詳見 Lilian's Blog）

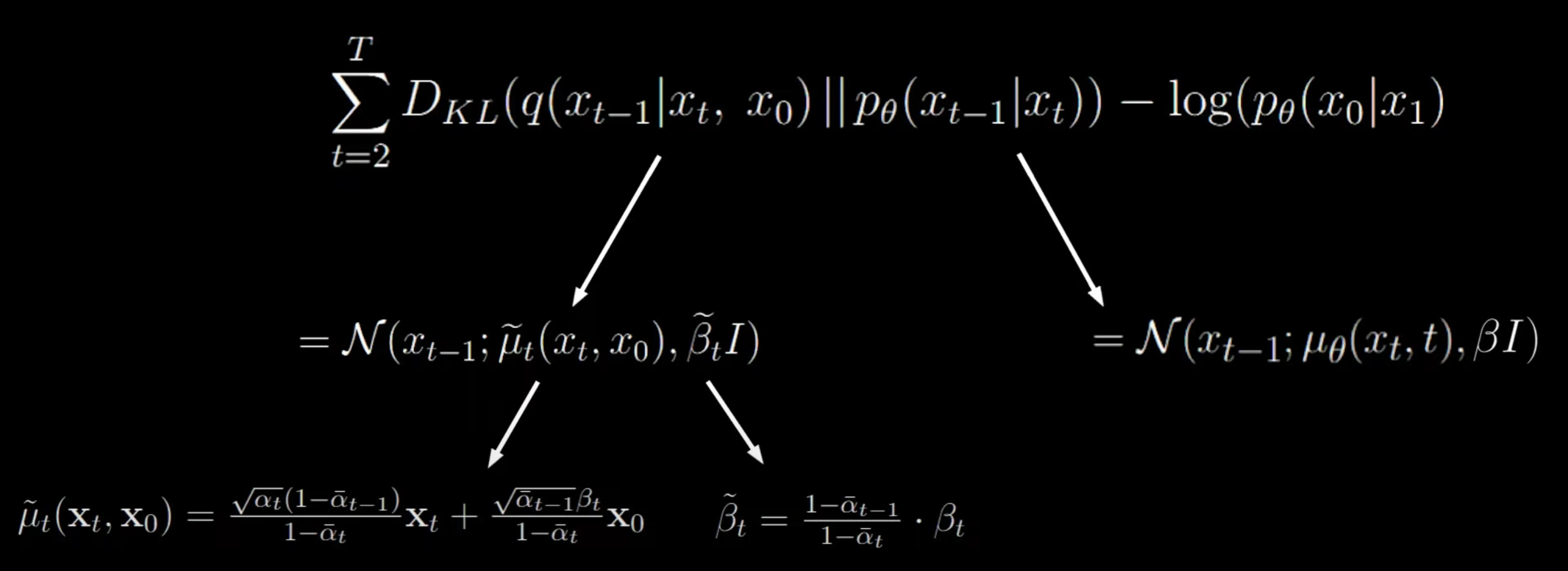
$\beta$ 是固定的，那麼就關注 $\mu$ 的形式：

正向過程生成的閉合形式 $x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon$ 可以重寫為 $x_0$ 形式：

將上述 $x_0$ 的表達式代入預測均值公式 $\tilde{\mu}_t$：

現在 $\mu$ 不再依賴 $x_0$。繼續化簡，首先展開第二項：

將 $x_t$ 項進行合併：

對 $x_t$ 的系數進行進一步合併和化簡，最終得到：

這表示我們基本上只是減去 $x_t$ 生成的隨機縮放噪聲，這就是神經網絡要預測的東西。

代入後的損失函數 $L_t$ 定義為一個均方誤差：

最後的形式就是時間步 $t$ 的實際噪聲和神經網絡預測噪聲之間的均方誤差。研究人員發現忽略前面的縮放項會得到更好的採樣質量並且更容易實現。

回到原始公式

作者決定在最後一步的採樣中，不再添加額外的隨機噪聲使生成過程更加穩定：

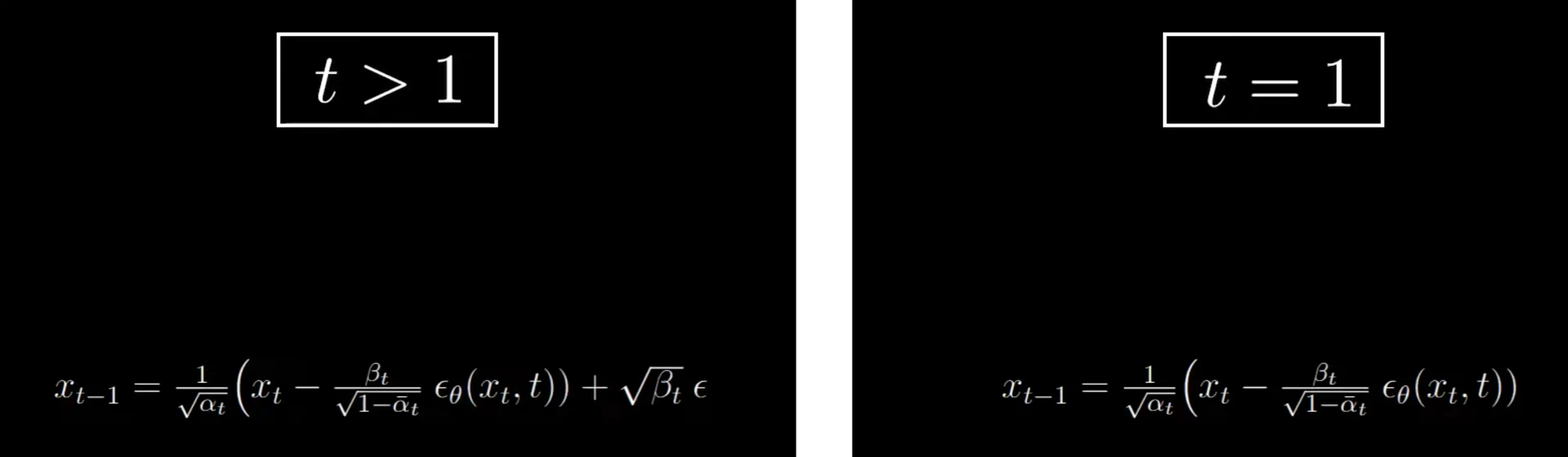
最後的形式為：

• $\mathbb{E}_{t, \mathbf{x}_0,\boldsymbol{\epsilon}}$ 表示對時間步 $t$、原始數據 $\mathbf{x}_0$ 和噪聲 $\boldsymbol{\epsilon}$ 取期望
• $\boldsymbol{\epsilon}$ 是實際添加的隨機噪聲
• $\boldsymbol{\epsilon}_\theta$ 是神經網絡預測的噪聲
• $\sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}$ 是前向過程的閉式解，表示在時間步 $t$ 的噪聲數據，因此可以簡化為：
  • $\mathbf{x}_t$ 直接表示時間步 $t$ 的噪聲數據，即 $\sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}$
  • 整個損失函數本質上是在衡量預測噪聲與實際噪聲之間的均方誤差

其中，時間步 $t$ 通常是從均勻分布中採樣的（即 $t∼Uniform(1,T)$，T 是總的時間步數）。這種選擇確保了在訓練過程中，每個時間步都有相同的概率被選擇，從而使模型在所有時間步上都能有效地學習去噪過程。

訓練#

首先我們從數據集中採樣一些圖像，然後採樣 $t$ 和來自正態分布的噪聲，然後通過梯度下降優化目標

採樣#

首先從正態分布中採樣 $x_t$，然後用前面展示過的公式通過重參數化來採樣 $x_{t-1}$。

注意這裡 $t=1$ 時是不增加噪聲的，根據公式

在 $t = 1$ 時，公式用於從 $x_1$ 恢復到 $x_0$，這是去噪過程的最後一步。此時，我們希望盡可能準確地重建原始圖像。在最後一步不添加噪聲（即沒有 $\sqrt{\beta_t} \epsilon$ 項），可以避免在生成最終圖像時引入不必要的隨機性，從而保持圖像的清晰度和細節。

代碼實現#

推薦 知乎 Sunrise 的 MLP 簡化實現
後面有時間的話考慮做一下 Stable Diffusion 的代碼手撕，挖個坑...

參考資料#

• Diffusion Models | Paper Explanation | Math Explained
• Lilian Weng: From Autoencoder to Beta-VAE
• Lilian Weng: What are Diffusion Models?